 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1636 | Gradito: |
Leggi anche appunti:Geometria: il limite euclideoGEOMETRIA: IL LIMITE EUCLIDEO La scienza è sempre stata considerata la Limite di una funzioneLimite di una funzione Per introdurre il concetto di limite di una funzione Differenziale di una funzioneDifferenziale di una funzione 1. Dimostrazione |
 |
 |
SIGNIFICATO GEOMETRICO DELL'INTEGRALE DI RIEMANN
L'integrale di Riemann di una funzione ha un notevole significato geometrico.
Per comprendere bene questa cosa è opportuno presentare due definizione:
Definizione 1.
Si chiama plurirettangolo ogni poligono che risulti essere un rettangolo oppure l'unione di un numero finito di rettangoli a due a due privi di punti interni comuni.
Ad esempio è un plurirettangolo l'insieme P.
area plurirettangolo P=areaR1(rettangolo1)+areaR2++areaRn
Definizione 2.
Sia f(x) una funzione reale definita in un intervallo compatto[a,b] di estremi non negativi.
Si chiama rettangoloide di base [a,b] relativo alla funzione f l'insieme dei punti (x,y) del piano cartesiano tali che :
a x b e 0 y f(x)
grafico cfr. pag 6
nel primo caso la funzione f è limitata in [a,b] nel secondo caso no,
In tale ipotesi, per ogni partizione P= di [a,b] la somma integrale inferiore
s(p)=![]()
rappresenta l'area del plurirettangolo, unione dei rettangoli R1,R2,..Rn.
Di base rispettivamente x1-x0, x2 -x1,, x n -x n-1
e altezza m0 ,m1, m2.mn . Tale plurirettangolo è contenuto nel rettangoloide R di base [a,b] relativo alla funzione f(x).
Analogalmente la somma integrale superiore:
S(p)=![]()
rappresenta l'area di un plurirettangolo contenente il rettangoloide R unione degli n rettangoli di base rispettivamente x1-x0, x2 -x1,, x n -x n-1 e altezza M0 ,M1, M2.Mn.
Al valore della partizione P di [a,b] gli insiemi numerici A= e B= rappresentano geometricamente l'insieme delle aree dei plurirettangoli contenuti nel rettangoloide R e l'insieme delle aree dei plurirettangoli contenuti in R.
Definizione 3.
Si dice che il rettangoloide R è dotato di area se gli insiemi numerici A e B delle aree dei plurirettangoli contenuti e contenenti R sono continui.
In tale ipotesi l'unico elemento separatore si chiama area del rettangoloide R.
Ne consegue intuitivamente , tenendo conto della definzione di integrale secondo Reimann il seguente risultato:
Significato geometrico dell'integrale di Reimann.
Se f(x) è una funzione non negativa e integrabile nell'intervallo [a,b] allora il rettangoloide R di base [a,b] relativo alla funzione f(x) è dotato di area che risulta:
![]()
area R=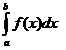
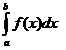
Osservazione(notevole).
Consideriamo una funzione reale f 0 in [a,b]. E' evidente che anche ora è preferibile definire il rettangoloide di base [a,b] relativo a f. si tratta dell'insieme dei punti (x,y) del piano cartesiano tali che:
xe[a,b] e f(x) y
Premesso ciò indichiamo con R il rettangoloide di base [a,b] relativo alla funzione f e con R' il rettangoloide di base [a,b] relativo alla funzione opposta '-f( 0 in [a,b]).
Poichè i rettangoloidi R e R' sono congruenti deve risultare
areaR=areaR'
D'altra parte sappiamo già che :
areaR'=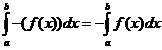
Si deduce quindi:
areaR=-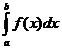
Quindi se f 0 in [a,b] l'integrale di f esteso ad [a,b] è opposto dell'area del rettangoloide di base [a,b] relativo a f.
 |
| Appunti su: |
|
| Appunti Geografia |  |
| Tesine Fisica |  |
| Lezioni Contabilita |  |