 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1958 | Gradito: |
Leggi anche appunti:La formula di taylorLA FORMULA DI TAYLOR Sia f(x) una funzione reale definita Un nuovo postulato delle paralleleUN NUOVO POSTULATO delle parallele Una trentina d'anni dopo la pubblicazione Geometria ellitticaGEOMETRIA ELLITTICA La seconda geometria non euclidea ha le stesse caratteristiche |
 |
 |
Sia f(x) una funzione reale definita in un
intorno I(![]() ) del punto
) del punto ![]() e derivabile in
e derivabile in ![]() . Consideriamo la differenza
. Consideriamo la differenza
![]()
Osserviamo che essendo
(**) 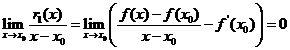
Tale funzione ha in ![]() un infinitesimo di
ordine superiore ad
un infinitesimo di
ordine superiore ad ![]() nel senso che
nel senso che ![]() tende a zero più rapidamente di
tende a zero più rapidamente di ![]() quando
quando ![]() .
.
Osservazione 1
È noto che in ogni approssimazione l'errore è definito da:
errore = valore vero - valore approssimato
conseguentemente ![]() rappresenta l'errore che si commette quando si assume
rappresenta l'errore che si commette quando si assume ![]() e cioè quando si
sostituisce il valore f(x) di f nel punto x con il valore in x del
polinomio di primo grado
e cioè quando si
sostituisce il valore f(x) di f nel punto x con il valore in x del
polinomio di primo grado ![]() .
.
Significato geometrico
Consideriamo il diagramma della funzione f e
il punto ![]() di tale diagramma. È noto che la retta tangente a tale
diagramma nel punto
di tale diagramma. È noto che la retta tangente a tale
diagramma nel punto ![]() ha equazione
ha equazione
![]()
Conseguentemente ![]() rappresenta la
differenza tra le ordinate del punto
rappresenta la
differenza tra le ordinate del punto ![]() del diagramma e del
punto ... della retta tangente
del diagramma e del
punto ... della retta tangente
Si nota dalla figura che la distanza verticale
tra la curva e la retta tangente quando x è abbastanza prossimo a ![]() è più piccola della
distanza di x da
è più piccola della
distanza di x da ![]() e cioè risulta
e cioè risulta
![]() per x abbastanza
prossimo a
per x abbastanza
prossimo a ![]()
Conseguentemente, dal punto di vista
geometrico, il limite (**).. Che la distanza verticale della curva della
tangente a cioè la funzione![]() tende a zero più rapidamente della distanza
tende a zero più rapidamente della distanza ![]() di x da
di x da ![]() quando x tende a
quando x tende a ![]()
È facile convincersi che tra tutte le rette
passanti per il punto![]() la tangente in
la tangente in ![]() è quella che
approssima meglio il diagramma
è quella che
approssima meglio il diagramma ![]() nei punti x vicini a
nei punti x vicini a ![]() . Se vogliamo approssimazioni migliori dobbiamo utilizzare
altre curve.
. Se vogliamo approssimazioni migliori dobbiamo utilizzare
altre curve.
A tale scopo, invece della tangente, adoperiamo la parabola
![]()
Consideriamo la funzione
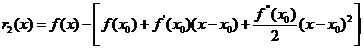
Applicando le regola di l' Hopital si ha
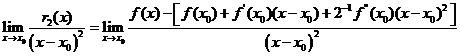
![]()
=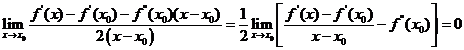
Dove certamente occorre supporre f derivabile
una volta in un intorno I(![]() ) di
) di![]() e due volte nel punto
e due volte nel punto ![]() .
.
Ne segue che ![]() tende a zero per
tende a zero per ![]() più rapidamente di
più rapidamente di ![]() e cioè del quadrato della distanza di x da
e cioè del quadrato della distanza di x da ![]() e si capisce che se x è abbastanza vicino a
e si capisce che se x è abbastanza vicino a ![]() risulta
risulta ![]() <
<![]() e dunque l'approssimazione ottenuta è migliore.
e dunque l'approssimazione ottenuta è migliore.
In generale, applicando ripetutamente n-1 volte la regola di l'Hopital si ottiene il seguente risultato
TEOREMA
Sia f(x) una funzione derivabile n-1 volte in
un intorno di ![]() e n volte nel punto
e n volte nel punto ![]() .
.
Considerata la differenza
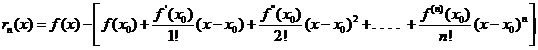
Dove con il simbolo n! si intende il
fattoriale di n e cioè il prodotto ![]() risulta
risulta
![]()
E cioè, come si suol dire, ![]() per
per ![]() è infinitesimo di
ordine superiore a
è infinitesimo di
ordine superiore a ![]() .
.
Ciò premesso si da la seguente
Definizione
Nelle ipotesi su f del teorema precedente, l'uguaglianza
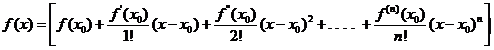
Si chiama formula di Taylor della
funzione f di punto iniziale ![]() .
.
Il polinomio di grado ![]()
![]()
Si chiama polinomio di Taylor di punto
iniziale ![]() .
.
La funzione ![]() che rappresenta l'errore che si commette quando si assume
che rappresenta l'errore che si commette quando si assume ![]() si chiama resto di Peano della formula di Taylor.
si chiama resto di Peano della formula di Taylor.
Se ![]() la formula di Taylor si chiama anche formula di McLaurin.
la formula di Taylor si chiama anche formula di McLaurin.
Osservazione 1
È utile tenere presente che se f(x) e g(x)
sono due infinitesime in ![]() in simboli
in simboli
![]()
Che si legge f è un o piccolo di g in ![]() , esprime che f(x) è in
, esprime che f(x) è in ![]() un infinitesimo di
ordine superiore a g(x) e cioè che risulti
un infinitesimo di
ordine superiore a g(x) e cioè che risulti
![]()
Utilizzando questa definizione, posto ![]() in virtù del teorema precedente la formula di Taylor può
riscriversi nella forma
in virtù del teorema precedente la formula di Taylor può
riscriversi nella forma
![]()
E esprime che la funzione f(x) si può
rappresentare in un intorno I(![]() ) come somma del suo polinomio di Taylor e di un infinitesimo
in
) come somma del suo polinomio di Taylor e di un infinitesimo
in ![]() di ordine superiore a
di ordine superiore a ![]()
Osservazione 2
È facile verificare, calcolando le derivate
della funzione considerate nel punto 0, che la formula di McLaurin di ![]() con n=3 sono:
con n=3 sono:
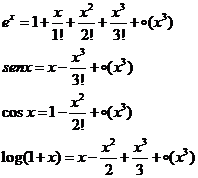
Tali espressioni possono essere utilizzate per il calcolo dei limiti in forma indeterminata.
Utilizzando la formula di Taylor è possibile dimostrare il seguente risultato che può essere utile nelle applicazioni.
TEOREMA condizione sufficiente di estremo relativo)
Sia f(x) una funzione derivabile una volta
nell'intervallo![]() e due volte nel punto
e due volte nel punto![]() V.s.i.
V.s.i.
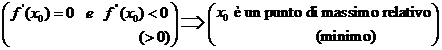
Dim
Consideriamo la formula di Taylor di f con n=2:
![]()
Tale formula, per le ipotesi, si può riscrivere nella forma
![]()
Dividendo per![]() e passando al limite per
e passando al limite per ![]() , si ha
, si ha
![]()
Conseguentemente, per il teorema della permanenza del segno,
![]()
L'uguaglianza è valida solo per ![]() .
.
Ma ciò significa, secondo definizione,che ![]() è un punto di massimo
relativo per f.
è un punto di massimo
relativo per f.
Il teorema è dimostrato.
 |
| Appunti su: |
|
| Appunti Fisica |  |
| Tesine Statistica |  |
| Lezioni Contabilita |  |