 |
|
 |
|
| Visite: 2207 | Gradito: |
Leggi anche appunti:TESI DI FINE ANNO - Dall'invenzione del telefono alla trasmissione datiTESI DI FINE ANNO Dall'invenzione del telefono alla trasmissione dati. SOMMARIO. Storia: Schema dell'apparecchio telefonicoSchema dell'apparecchio telefonico In Fig. è riportato lo schema di un apparecchio Comportamento della modulazioneComportamento della modulazione Bisogna adattare le caratteristiche dello |
 |
 |
COMUNICAZIONI PUNTO-PUNTO:
RIVELAZIONE, DIVERSITA' E INCERTEZZA DI CANALE
Introduzione
Il nostro obiettivo è quello di affrontare in questo lavoro i problemi che nascono nelle comunicazioni su canali in cui è presente FADING.
Questo ci induce ad investigare sulle varie tecniche, cosiddette di diversità, che ci consentono di migliorare la nostra performance.
Le tecniche in diversità agiscono sul tempo, frequenza o spazio, ma l'idea di base è la stessa.
Inviando segnali, che portano la stessa informazione attraverso cammini diversi, siamo in grado di ottenere al ricevitore molteplici repliche indipendenti e attenuate di simboli e di raggiungere una rivelazione più affidabile.
Il più semplice schema in diversità usa il codice di ripetizione.
Schemi più sofisticati sfruttano la diversità di canale, e al tempo stesso, usano in maniera efficiente i gradi di libertà nel canale.
In confronto al codice a ripetizione questi schemi forniscono guadagni di codice oltre a guadagni in diversità.
Nella diversità in frequenza, consideriamo tre casi:
portante singola con equalizzazione di interferenza intersimbolica,
spettro espanso a sequenza diretta,
multiplexing a divisione a frequenza ortogonale.
Rivelazione in un canale soggetto a fading di Rayleigh
Rivelazione non coerente
Cominciamo con un semplice problema di rivelazione in un canale con fading.
Per semplicità, assumiamo un modello di fading di Rayleigh piatto dove
il canale può essere rappresentato da una singola presa ![]() di un filtro complesso
tempo discreto, che possiamo abbreviare come
di un filtro complesso
tempo discreto, che possiamo abbreviare come ![]() :
:
![]() ,
,
dove ![]()
![]()
Per il momento, comunque, noi non specifichiamo la dipendenza tra i
coefficienti di fading ![]() ad istanti
ad istanti ![]() diversi, né facciamo
alcuna assunzione sulla conoscenza a priori che il ricevitore potrebbe avere di
diversi, né facciamo
alcuna assunzione sulla conoscenza a priori che il ricevitore potrebbe avere di
![]() . (Quest'ultima assunzione è a volte detta comunicazione non coerente.)
. (Quest'ultima assunzione è a volte detta comunicazione non coerente.)
Si assume ![]() e
e ![]() .
.
Prima consideriamo una segnalazione antipodale binaria (o binary
phase-shift keying, BPSK) non codificata con ampiezza a, ![]() , in cui i simboli
, in cui i simboli ![]() sono indipendenti dal
tempo.
sono indipendenti dal
tempo.
Questo tipo di segnalazione fallisce completamente, anche in assenza di
rumore, dal momento che la fase del
segnale ricevuto ![]() è uniformemente distribuita tra 0 e
è uniformemente distribuita tra 0 e ![]() a prescindere che sia
trasmesso
a prescindere che sia
trasmesso ![]() o
o ![]() , ed anche l'ampiezza
è indipendente dal simbolo trasmesso.
, ed anche l'ampiezza
è indipendente dal simbolo trasmesso.
Dovremo pensare ad una segnalazione che abbia un particolare tipo di codice tra i simboli.
Possiamo considerare una semplice modulazione
ortogonale, dove in due diversi tempi di campionamento trasmettiamo ![]() o
o ![]() .
.
Quello che vogliamo ottenere è una
rivelazione basata su 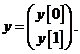
In questo tipo di problemi dove la decisione si basa su delle ipotesi torna utile ricordarci il criterio della massima verosimiglianza (maximum likelihood):
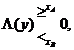
dove ![]() è il rapporto
log-likelihood
è il rapporto
log-likelihood

Si può vedere che, se viene trasmesso![]() ,
, ![]()
![]() e
e![]()
![]() , analogamente se viene trasmesso
, analogamente se viene trasmesso ![]() ,
, ![]()
![]() e
e![]()
![]() .
.
Inoltre, ![]() e
e ![]() sono indipendenti, per
cui il rapporto log-likelihood può essere calcolato come:
sono indipendenti, per
cui il rapporto log-likelihood può essere calcolato come:
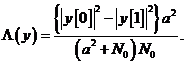
Il criterio di decisione ottimo è decidere ![]() , se
, se ![]() , e decidere
, e decidere ![]() , altrimenti.
, altrimenti.
Come si osserva, il criterio non fa uso delle
fasi del segnale ricevuto, dal
momento che, le fasi dei guadagni di canale ![]()
![]() , essendo casuali e non note sarebbero inutili per la
rivelazione.
, essendo casuali e non note sarebbero inutili per la
rivelazione.
La probabilità di errore calcolata per integrazione diretta è:
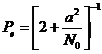 .
.
SNR = -------- ----- ------ -------- ----- ------ ----- ----- ----------
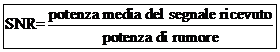
![]()
![]()
|
La potenza di rumore per tempo di simbolo è ![]() .
.
Per lo schema di modulazione ortogonale che
abbiamo visto or ora, la potenza media ricevuta per tempo di simbolo è ![]() , perciò SNR
, perciò SNR![]() e andando a sostituire nell'espressione della
e andando a sostituire nell'espressione della ![]() otteniamo:
otteniamo:
![]()
Questo risultato è scoraggiante poiché, avere
una probabilità di errore ![]() , richiederebbe un SNR
, richiederebbe un SNR![]() (27 dB).
(27 dB).
Sarebbe necessaria una potenza enorme per ottenere una comunicazione affidabile.
Rivelazione coerente
I pessimi risultati che si ottengono con la rivelazione non coerente risultano evidenti osservando che, mentre la probabilità d'errore con questo tipo di rivelazione decade in modo inversamente proporzionale ad SNR, la probabilità d'errore in un canale AWGN decade addirittura esponenzialmente con SNR.
Per avere una probabilità di errore di ![]() , c'è bisogno di solo un SNR
, c'è bisogno di solo un SNR![]() 7 dB in un
canale AWGN (da confrontare con i 27 dB del canale con fading non-coerente).
7 dB in un
canale AWGN (da confrontare con i 27 dB del canale con fading non-coerente).
Se confrontiamo la rivelazione in un canale AWGN con la rivelazione non coerente di un canale con fading osserviamo due differenze:
i guadagni di canale ![]() sono casuali,
sono casuali,
il ricevitore non conosce tali guadagni.
Supponiamo ora che i guadagni di canale siano noti al ricevitore, ma ancora casuali.
In pratica questo viene fatto o inviando una sequenza nota detta pilota, oppure attraverso un metodo diretto dalle decisioni, in cui la stima di canale viene fatta usando simboli usati in precedenza.
L'accuratezza dell'inseguimento dei guadagni da parte del ricevitore dipende, naturalmente, dalla velocità con cui varia il canale.
Conoscendo i guadagni di canale, la rivelazione, che sarà perciò coerente del BPSK può essere rappresentata simbolo per simbolo.
Nella figura 1.1 vengono confrontate le probabilità di errore del BPSK coerente, quelle della segnalazione ortogonale non-coerente su canale soggetto a fading di Rayleigh, e quelle per il BPSK sul canale AWGN.
|
|
Figura 1.1 - Confronto tra la probabilità di errore di una rivelazione coerente, non coerente e di un canale AWGN non attenuato |
Osserviamo che mentre la probabilità d'errore per il BPSK su canale AWGN decade molto velocemente con SNR, le probabilità d'errore per il canale con fading di Rayleigh sono molto peggiori, sia che la rivelazione sia coerente o non-coerente.
Ad una prima grossolana valutazione si può dire che la rivelazione coerente decade in modo inversamente proporzionale a SNR, così come la segnalazione ortogonale non-coerente.
Andando ad osservare il valore, seppur
approssimato, della ![]() nel caso coerente esso vale
nel caso coerente esso vale ![]() , mentre nel caso non-coerente
vale
, mentre nel caso non-coerente
vale ![]() .
.
C'è una differenza di 3 dB in termini di SNR tra i due casi, che è comunque poca cosa!
Ne deriva allora che, la ragione principale per cui la rivelazione nel canale con fading fornisce una bassa performance non è la assenza di conoscenza del canale al ricevitore.
Essa risiede nel fatto che il guadagno di canale è casuale e c'è una forte probabilità che il canale sia in uno stato di "profonda attenuazione".
Questa probabilità ha lo stesso ordine di grandezza della probabilità d'errore.
Possiamo concludere che ad alti SNR gli "errori" sono per lo più causati dal fatto che il canale è molto attenuato e non perché il rumore additivo è grande.
Dal BPSK al QPSK: sfruttando i gradi di libertà
La modulazione BPSK (![]() ) usa solo la dimensione reale (il canale I), mentre in pratica
sia il canale I che il canale Q vengono usati simultaneamente nelle
comunicazioni coerenti, aumentando l'efficienza spettrale.
) usa solo la dimensione reale (il canale I), mentre in pratica
sia il canale I che il canale Q vengono usati simultaneamente nelle
comunicazioni coerenti, aumentando l'efficienza spettrale.
Usando la modulazione QPSK (quadrature-phase-shift-keying) può venire trasmesso un bit in più; per esempio la costellazione può essere:
![]()
Dal momento che il rumore è indipendente sui canali I e Q, i bits possono essere rivelati separatamente e la probabilità di errore del bit sul canale AWGN è
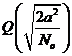 ,
,
esattamente come nel caso BPSK.
Definendo il SNR per il BPSK come:
![]() ,
,
mentre per il QPSK,
![]() ,
,
è due volte quello del BPSK dal momento che vengono usati entrambi i canali I e Q.
Equivalentemente, per un dato SNR, la probabilità di errore sul bit
di un BPSK è ![]() e quella di QPSK è
e quella di QPSK è ![]() .
.
La probabilità di errore di QPSK, in un
canale soggetto a fading di Rayleigh, può
ottenersi rimpiazzando ![]() al posto di
al posto di ![]() nell'espressione della
probabilità di errore coerente del
BPSK:
nell'espressione della
probabilità di errore coerente del
BPSK:
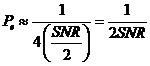
Un punto importante degno di nota è che dall'uso di entrambi i canali I e Q è possibile ottenere una efficienza energetica molto maggiore rispetto all'uso di ciascuno di loro.
La perdita di un caso rispetto all'altro è dovuta al fatto che è molto più efficiente concentrare energia, per una distanza di separazione minima data, in un numero di punti della costellazione a più alta dimensione spaziale rispetto ad una più bassa.
Siamo così giunti a poter enunciare una generale dichiarazione di principio:
|
Un buono schema di comunicazione sfrutta TUTTI i gradi di libertà disponibili nel canale |
Diversità
Alcuni degli schemi considerati sono più efficienti di altri da un
punto di vista spettrale, ma da un punto di vista pratico sono tutti scadenti:
la loro probabilità di errore decade molto lentamente, come ![]() .
.
Avevamo visto che la causa di fondo di questa scarsa performance è che, l'affidabilità della comunicazione dipende dal tipo di cammino di ogni singolo segnale.
C'è una significativa probabilità che questo cammino si trovi in uno stato di intensa attenuazione.
In tale stato, qualsiasi schema di comunicazione soffrirà della presenza di errori.
Una soluzione naturale per migliorare la performance è assicurare che i simboli di informazione passino attraverso segnali multipli, ognuno dei quali ha una attenuazione indipendente, assicurando una comunicazione affidabile quando lo sia almeno uno dei cammini.
Questa tecnica è chiamata diversità, e può migliorare enormemente la performance dei canali con fading.
Ci sono molti modi per realizzare la diversità.
La diversità nel tempo può realizzarsi tramite coding o interleaving: l'informazione è codificata e i simboli di codice sono distribuiti nel tempo in intervalli di coerenza diversi, cosicché alcune parti delle parole di codice incontrano attenuazioni indipendenti.
Analogamente, è possibile anche sfruttare diversità in frequenza, se il canale è selettivo in frequenza.
In un canale con antenne trasmittenti multiple o antenne riceventi sufficientemente spaziate, la diversità può ottenersi pure nello spazio.
In una rete cellulare, la macrodiversità è sfruttata quando un segnale che viene inviato da un mezzo mobile può essere ricevuto da due stazioni base.
Dal momento che la diversità è una risorsa così importante, un sistema wireless si serve tipicamente di alcuni tipi di diversità.
Parlando di tecniche in diversità nel tempo, nello spazio, in frequenza cominciamo da un semplice schema basato sul codice a ripetizione: lo stesso simbolo di informazione viene trasmesso sui cammini di alcuni segnali.
Se il codice a ripetizione riesce a raggiungere il massimo guadagno in diversità, esso è però "dispendioso" in termini di uso di gradi di libertà del canale.
Schemi più sofisticati possono aumentare la velocità dei dati ed ottenere un guadagno di codice insieme al guadagno in diversità.
Proponendoci di studiare uno scenario coerente osserveremo il caso in cui il ricevitore ha una perfetta conoscenza dei guadagni di canale e può combinare coerentemente i segnali ricevuti sui differenti cammini.
Questa conoscenza viene appresa via training cioè attraverso una sequenza pilota di simboli e la precisione dipende dal tempo di coerenza del canale e dalla potenza ricevuta del segnale trasmesso.
Diversità nel tempo
La diversità nel tempo si ottiene facendo la media nel tempo dell'attenuazione del canale.
Tipicamente, il tempo di coerenza del canale è dell'ordine di 10![]() 100 simboli, e perciò il canale è fortemente correlato
attraverso simboli consecutivi.
100 simboli, e perciò il canale è fortemente correlato
attraverso simboli consecutivi.
Per assicurare che simboli codificati siano trasmessi attraverso guadagni attenuati indipendenti, si rende necessario l'interleaving delle parole di codice.
Per semplicità consideriamo un canale con fading piatto.
Trasmettiamo una parola di codice x
= ![]() di lunghezza L
simboli e il segnale ricevuto è dato da
di lunghezza L
simboli e il segnale ricevuto è dato da
![]()
![]()
Applicando un interleaving ideale, così che i simboli consecutivi ![]() vengano trasmessi
sufficientemente separati nel tempo, possiamo assumere che
vengano trasmessi
sufficientemente separati nel tempo, possiamo assumere che ![]() siano indipendenti.
siano indipendenti.
Il parametro L è comunemente chiamato il numero di rami in diversità.
Il rumore additivo è costituito da variabili casuali ![]() i.i.d.
i.i.d.
Esistono vari tipi di codice, ma è possibile affermare che il codice più semplice possibile è il codice a ripetizione.
Sebbene realizzi un guadagno in diversità, non sfrutta i gradi di libertà effettivamente disponibili nel canale, perché ripete banalmente lo stesso simbolo su L tempi di simbolo.
|
|
|
Figura 1.2 - Trasmissione di parole di codice con e senza INTERLEAVING |
Esistono anche codici più efficienti che sfruttano meglio i gradi di libertà disponibili e sono detti codici a rotazione.
|
|
|
|
Figura 1.3a - Codice di rotazione |
Figura 1.3b - Codice di ripetizione |
Diversità d'antenna
Per sfruttare la diversità di tempo, è necessario l'interleaving e la codifica su un tempo di coerenza di alcuni periodi.
Quando c'è un ritardo limitato e/o il tempo di coerenza è grande, questo non è possibile.
In questo caso dobbiamo pensare ad altre forme di diversità.
Diversità d'antenna, o diversità spaziale si possono ottenere sistemando antenne multiple al trasmettitore e/o al ricevitore.
Se le antenne sono disposte in modo abbastanza separato, i guadagni di canale tra coppie di antenne differenti si attenuano più o meno indipendentemente e vengono creati nuovi cammini per il segnale.
La necessaria separazione di antenna dipende dallo scatteramento dell'ambiente locale e dalla frequenza portante.
Per un mezzo mobile che si trova vicino al terreno, con molti scatteratori nelle vicinanze, il segnale si scorrela su modeste distanze spaziali ed è sufficiente una tipica separazione d'antenna di mezza lunghezza d'onda.
Per stazioni base disposte su alte torri, può essere richiesta una più larga separazione d'antenna, di una decina di lunghezze d'onda.
Distinguiamo la ricezione in diversità, che fa uso di molteplici antenne riceventi (single input multiple output ovvero canali SIMO), e la trasmissione in diversità, che fa uso di molteplici antenne trasmittenti (multiple input single output ovvero canali MISO).
Canali con antenne multiple sia in ricezione che in trasmissione (multiple input multiple output ovvero canali MIMO) sviluppano una potenzialità ed efficienza ancora maggiore.
Oltre ad incrementare la diversità, i canali MIMO forniscono un aumento di gradi di libertà per la comunicazione.
Ricezione in diversità
In un canale con fading piatto con 1 antenna trasmittente e L antenne riceventi, il modello di canale è del tipo:
![]()
![]()
dove il rumore ![]()
![]() è indipendente tra le antenne.
è indipendente tra le antenne.
|
|
|
Figura 1.4 - Ricezione in diversità |
Quello che vogliamo fare, è rivelare ![]() basandoci su
basandoci su ![]() .
.
Questo è esattamente lo stesso problema di rivelazione che si ha nell'uso del codice a ripetizione e interleaving sul tempo, con L rami in diversità sullo spazio, piuttosto che sul tempo.
Se le antenne sono sufficientemente separate nello spazio, possiamo
assumere che i guadagni ![]() siano indipendenti e
di Rayleigh, e avremo un guadagno in diversità di L.
siano indipendenti e
di Rayleigh, e avremo un guadagno in diversità di L.
Con la ricezione in diversità, ci sono di fatto due tipi di guadagni all'aumentare di L.
Il primo guadagno corrisponde ad un guadagno di potenza (detto altresì guadagno di array): avendo antenne riceventi multiple e una combinazione coerente al ricevitore, l'effettiva potenza totale del segnale ricevuto aumenta linearmente con L.
Il secondo guadagno corrisponde ad un guadagno in diversità: mediando sopra i cammini multipli e indipendenti di segnale, la probabilità che l'intero guadagno sia piccolo diminuisce.
Trasmissione in diversità
Consideriamo ora il caso in cui ci siano L antenne trasmittenti ed 1 antenna ricevente, il canale MISO.
|
|
|
Figura 1.5 - Trasmissione in diversità |
Questo schema è adatto al downlink di un sistema cellulare, dal momento che, è spesso più economico avere antenne multiple alla stazione base piuttosto che averle ad ogni mezzo mobile.
E' semplice avere un guadagno in diversità di L: semplicemente trasmettendo lo stesso simbolo su L antenne differenti durante L tempi di simbolo.
Ad ogni istante, solo una antenna è accesa, mentre le altre sono spente.
Questo è semplicemente un codice a ripetizione, e, come è noto, i codici a ripetizione "sprecano" per così dire molti gradi di libertà.
Più in generale, ogni codice a blocco di lunghezza L in diversità di tempo può essere usato su questo sistema di trasmissione in diversità: semplicemente accendendo una antenna ad un istante e trasmettendo in successione sulle altre differenti antenne i simboli codificati del codice in diversità di tempo.
Questo produce un guadagno di codice rispetto al codice a ripetizione.
E' possibile anche progettare codici specificamente per sistemi di trasmissione in diversità.
Ci sono state molte ricerche su questo tema della codifica spazio-tempo, a partire dalla più nota e semplice, il così detto schema Alamouti.
Questo schema di trasmissione in diversità è usato in alcuni standard di terza generazione cellulare.
SCHEMA ALAMOUTI
Nel caso di fading piatto, il canale con due antenne trasmittenti e singola antenna ricevente è scritta come
![]()
dove ![]() è il guadagno di
canale dell'antenna trasmittente
è il guadagno di
canale dell'antenna trasmittente ![]() .
.
Lo schema Alamouti trasmette due simboli complessi ![]() e
e ![]() su due tempi di
simbolo:
su due tempi di
simbolo:
all'istante 1,
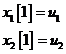
all'istante 2,
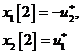
Se assumiamo che il canale rimanga costante su due tempi di simbolo e poniamo
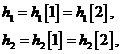
allora possiamo scrivere in forma matriciale:
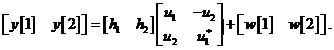
Poiché siamo interessati a rivelare ![]() riscriviamo questa
equazione come
riscriviamo questa
equazione come
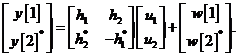
Osserviamo che le colonne della matrice quadrata sono ortogonali.
Di qui, il problema di rivelazione di ![]() si scompone in due
problemi separati e ortogonali.
si scompone in due
problemi separati e ortogonali.
Proiettiamo y su ognuna delle due colonne per ottenere le statistiche sufficienti
![]() i = 1,2,
i = 1,2,
dove ![]() e
e ![]()
![]() e
e ![]() sono indipendenti.
sono indipendenti.
Così, il guadagno in diversità è 2 per la rivelazione di ogni simbolo.
In confronto al codice a ripetizione, adesso vengono trasmessi due simboli su due tempi di simbolo anziché uno, ma con metà della potenza per ogni simbolo (assumendo che la potenza totale trasmessa è la stessa in entrambi i casi).
Esempio di un sistema MIMO 2x2
Consideriamo adesso un canale MIMO con due antenne trasmittenti e due antenne riceventi.
|
|
|
Figura 1.6 - Trasmissione e ricezione in diversità |
Sia ![]() il guadagno di canale
distribuito secondo Rayleigh dall'antenna trasmittente j all'antenna ricevente i.
il guadagno di canale
distribuito secondo Rayleigh dall'antenna trasmittente j all'antenna ricevente i.
Supponiamo che, sia le antenne trasmittenti che quelle riceventi siano
sufficientemente separate, così che i guadagni di canale,![]() , possano essere assunti indipendenti.
, possano essere assunti indipendenti.
Ci sono quattro cammini indipendenti e attenuati del segnale tra il trasmettitore e il ricevitore, ciò suggerisce che il massimo guadagno in diversità che può essere raggiunto è appunto quattro.
Anche lo stesso schema a ripetizione già visto può arrivare a questa performance: trasmette lo stesso simbolo su due antenne in due tempi di simbolo consecutivi (in ogni istante non viene mandato niente sull'altra antenna).
Se il simbolo trasmesso è![]() , i simboli ricevuti alle due antenne riceventi sono
, i simboli ricevuti alle due antenne riceventi sono
![]()
![]()
al primo istante, e
![]()
![]()
al secondo istante.
Effettuando una combinazione a massimo rapporto segnale-rumore dei 4
simboli ricevuti, si può dire che il guadagno effettivo di canale è ![]() , che porta a 4 il guadagno in diversità.
, che porta a 4 il guadagno in diversità.
Comunque, come nel caso del canale ![]() , lo schema a ripetizione utilizza malamente i gradi di
libertà nel canale, cioè trasmette solo un simbolo per due tempi di simbolo.
, lo schema a ripetizione utilizza malamente i gradi di
libertà nel canale, cioè trasmette solo un simbolo per due tempi di simbolo.
A questo riguardo lo schema Alamouti è più efficiente trasmettendo due simboli in due tempi di simbolo.
Ci domandiamo adesso se lo schema Alamouti utilizzi tutti i gradi di
libertà disponibili in un canale ![]() .
.
Ricordiamo che i gradi di libertà del canale rappresentano la dimensione del segnale ricevuto.
In un canale con due antenne trasmittenti e una sola antenna ricevente, avremo un grado di libertà per ogni tempo di simbolo.
Lo schema a ripetizione utilizza solo mezzo grado di libertà per ogni tempo di simbolo, mentre lo schema Alamouti ne utilizza uno intero.
Con L ricevitori, ma una singola antenna trasmittente, il segnale ricevuto giace in un vettore spaziale L dimensionale, ma non lo utilizza interamente.
Per vedere questo esplicitamente, consideriamo il seguente modello di canale:
![]()
dove y=![]() ,
, ![]() e
e ![]() .
.
Il segnale di interesse, ![]() , giace nello spazio ad una dimensione.
, giace nello spazio ad una dimensione.
Così possiamo concludere che, nel caso di ricevitore multiplo con singola antenna trasmittente, abbiamo un canale con un grado di libertà per tempo di simbolo.
Invece in un canale ![]() , ci sono potenzialmente due
gradi di libertà per tempo di simbolo.
, ci sono potenzialmente due
gradi di libertà per tempo di simbolo.
Per vedere ciò possiamo scrivere il canale come
![]()
dove ![]() e
e ![]() sono il simbolo
trasmesso e il vettore del guadagno di canale dell'antenna trasmittente
sono il simbolo
trasmesso e il vettore del guadagno di canale dell'antenna trasmittente ![]() , così come
, così come ![]() e
e![]() sono i vettori dei segnali ricevuti e il rumore.
sono i vettori dei segnali ricevuti e il rumore.
I canali ![]() e
e ![]() sono linearmente
indipendenti, quindi il segnale è a due dimensioni: il segnale dell'antenna
trasmittente
sono linearmente
indipendenti, quindi il segnale è a due dimensioni: il segnale dell'antenna
trasmittente ![]() arriva nella sua
direzione
arriva nella sua
direzione ![]() , e con due antenne riceventi, il ricevitore può distinguere
tra i due segnali.
, e con due antenne riceventi, il ricevitore può distinguere
tra i due segnali.
In confronto ad un canale![]() , c'è un grado di libertà in più.
, c'è un grado di libertà in più.
|
|
|
|
Figura 1.7a - Segnale monodimensionale |
Figura 1.7b - Segnale bidimensionale |
Né lo schema a ripetizione, né
lo schema Alamouti utilizzano tutti i
gradi di libertà di un canale 2![]() 2.
2.
Uno schema molto semplice è quello in cui vengono trasmessi simboli non codificati indipendenti su differenti antenne come pure su differenti tempi di simbolo.
Questo è un esempio di schema multiplexing spaziale: flussi di dati indipendenti sono multiplexati nello spazio.(Viene anche detto V-BLAST in letteratura.)
V-BLAST è l'acronimo di Vertical Bell Labs Space-Time Architecture.
D'altro canto, il pieno uso di gradi di libertà spaziali dovrebbe consentire un più efficiente 'impacchettamento' di bits, che dà come risultato un miglior guadagno di codice.
Possiamo trarre due indicazioni dallo schema V-BLAST.
Dapprima osserviamo un nuovo ruolo per le antenne multiple: oltre alla diversità, possiamo avere anche dei gradi di libertà in più per la comunicazione.
Questo è in un certo senso un modo più potente di sfruttare le antenne multiple.
Secondariamente lo schema rivela anche limitazioni nella nostra analisi di performance della struttura per codici spazio-tempo.
Finora il nostro approccio è stato quello di ricercare schemi che 'estraggano' la massima diversità dal canale e successivamente confrontarli sulla base del guadagno di codice, che è una funzione di come gli schemi utilizzano con efficienza i gradi di libertà disponibili.
Questo approccio si rivela insoddisfacente confrontando lo schema V-BLAST e lo schema Alamouti: lo schema V-BLAST ha una diversità inferiore dell'Alamouti, ma è più efficiente nello sfruttare gradi di libertà spaziali, ottenendo un miglior guadagno di codice.
Un vantaggio dello schema Alamouti è la ridotta complessità del ricevitore ML che decodifica le coppie di simboli in due problemi di rivelazione ortogonali a singolo simbolo.
La rivelazione ML dello schema V-BLAST non gode dello stesso vantaggio, poiché è necessaria la rivelazione contemporanea dei due simboli.
La complessità cresce esponenzialmente con il numero delle antenne.
Diversità in frequenza
Concetti di base
I canali a banda stretta con fading piatto sono modellati da un filtro a presa singola, in quanto la maggior parte dei cammini multipath arrivano durante un tempo di simbolo.
Nei canali a banda larga, invece, il segnale trasmesso arriva su più tempi di simbolo e i multipath possono essere distinti al ricevitore.
La risposta in frequenza non è più piatta, per esempio, la banda di
trasmissione ![]() è più larga della
banda di coerenza
è più larga della
banda di coerenza ![]() del canale.
del canale.
Questo produce un'altra forma di diversità:
Cominciamo con un modello di canale wireless in banda base tempo-discreto.
L'uscita campionata può essere scritta come
![]()
Qui ![]() indica la l-esima presa del filtro del canale
all'istante m.
indica la l-esima presa del filtro del canale
all'istante m.
Per capire il concetto di diversità in frequenza nell'accezione più
semplice, consideriamo prima il tipo di comunicazione in cui viene inviato un
simbolo ![]() in un sol colpo
all'istante 0, e nessun altro simbolo viene trasmesso dopo di quello.
in un sol colpo
all'istante 0, e nessun altro simbolo viene trasmesso dopo di quello.
Il ricevitore osserva
![]()
![]()
Se assumiamo che la risposta del canale abbia un numero finito di prese
L, allora le repliche ritardate del
segnale producono L rami in diversità
nel rivelare ![]() dal momento che i guadagni
dal momento che i guadagni ![]() sono assunti essere
indipendenti.
sono assunti essere
indipendenti.
Questa diversità si ottiene dalla capacità di distinguere cammini multipath al ricevitore grazie alla natura a larga banda del canale, ed è così chiamata diversità in frequenza.
Un semplice schema di comunicazione può essere costruito su tale idea, inviando un simbolo di informazione ogni L tempi di simbolo.
Possiamo ottenere un guadagno in diversità fino a L, ma il problema con questo schema è che c'è un notevole spreco di gradi di libertà: solo un simbolo può venire trasmesso per ogni delay spread.
Questo schema può pensarsi come l'analogo del codice a ripetizione usato per la diversità di tempo e di spazio, dove un simbolo di informazione è ripetuto L volte.
In questo scenario, se si cerca di trasmettere i simboli più frequentemente si incorre nella ben nota interferenza inter-simbolica (ISI): le repliche ritardate dei simboli precedenti interferiscono con il simbolo corrente.
Il problema sarà quindi quello di trattare con l'ISI e al tempo stesso sfruttare la diversità in frequenza nel canale.
Vengono comunemente suggeriti tre approcci:
Sistemi a singola portante con equalizzazione
Quello che vogliamo fare è risalire ad ogni simbolo del segnale trasmesso partendo dal segnale ricevuto.
Il processo di estrazione dei simboli dal segnale ricevuto è detto equalizzazione.
Usando la sequenza di rivelazione a massima
verosimiglianza (MLSD), la piena diversità di ![]() si può raggiungere per
una trasmissione non codificata inviata a tempo di simbolo, dove l'ISI è
significativa.
si può raggiungere per
una trasmissione non codificata inviata a tempo di simbolo, dove l'ISI è
significativa.
La rivelazione ottima ML dei simboli trasmessi può essere implementata usando l'Algoritmo di Viterbi.
Comunque, la complessità dell'Algoritmo di Viterbi cresce esponenzialmente con il numero di prese, ed è usato tipicamente quando il numero di prese significative è piccolo.
Alternativamente, si può ricorrere ad un equalizzatore lineare che rivela il simbolo corrente sopprimendo l'interferenza dagli altri simboli, ed ha un ordine più basso di complessità.
Spettro espanso a sequenza diretta
Con questo metodo, i simboli
di informazione sono codificati e modulati da una sequenza di pseudo-rumore e
trasmessi su un'ampiezza di banda ![]() più larga della
velocità dei dati.
più larga della
velocità dei dati.
Rispetto al caso in cui ogni simbolo indipendente viene inviato ad ogni tempo di simbolo, il data rate R (bits/s) in un sistema a spettro espanso, è tipicamente molto più piccolo della larghezza di banda di trasmissione W (Hz).
Quindi, molto pochi bits vengono trasmessi per grado di libertà e per ciascun utilizzatore.
Si conclude che, poiché la velocità di simbolo è molto bassa in un sistema a spettro espanso, l'ISI è praticamente trascurabile e l'equalizzazione non è richiesta.
Sebbene questo porti ad una utilizzazione inefficiente dei gradi di libertà totali nel sistema nella prospettiva che ci sia un solo utilizzatore, questo schema consente a molti utilizzatori di condividere i gradi di libertà totali, con gli utilizzatori che appaiono come fossero pseudorumore tra loro stessi.
I suoi componenti di base sono mostrati in figura 1.8.
|
|
|
Figura 1.8 - Direct Sequence Sprad-Spectrum |
Sistemi multiportante
Qui, la precodifica trasmessa è fatta per convertire il canale ISI in un set di sottoportanti ortogonali non-interferenti, ognuna delle quali aventi banda stretta su fading piatto.
La trasformazione tra il dominio del tempo e quello della frequenza viene fatto aggiungendo e sottraendo un prefisso ciclico e attraverso le operazioni IDFT/DFT.
Questo porta ad avere tempi morti in ordine al tempo e alla frequenza.
La diversità in frequenza può essere ottenuta codificando su sottoportanti diversamente attenuate.
Questo viene anche detto Discrete Multi-tone (DMT) o Orthogonal Frequency Division Multiplexing (OFDM).
La complessità è condivisa tra il trasmettitore e il ricevitore nelle operazioni IDFT/DFT.
La complessità di queste
operazioni è indipendente dal numero delle prese, varia poco in funzione delle
sottoportanti ![]() , ed è adatta ad essere implementata dalla attuale
tecnologia.
, ed è adatta ad essere implementata dalla attuale
tecnologia.
La complessità della diversità di codice attraverso le sottoportanti va di pari passo con la misura della quantità di diversità desiderata.
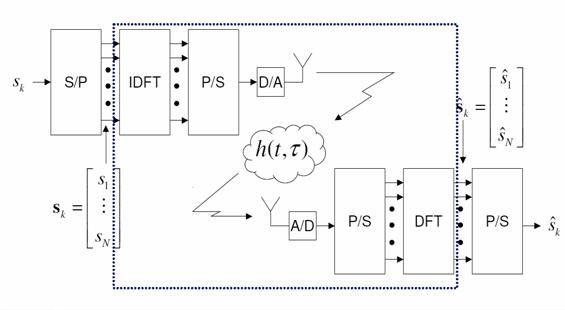
Figura 1.9 - Schema OFDM
Il GSM per esempio è un sistema a singola portante, mentre il CDMA è basato su una sequenza diretta a spettro espanso.
Un importante punto concettuale è che, mentre la diversità in frequenza è qualcosa di intrinseco in un canale a larga banda, la presenza dell'ISI non lo è, poiché dipende dalla tecnica di modulazione usata.
Per esempio, nella OFDM non c'è ISI, ma sottoportanti che, separate di più della banda di coerenza, vengono attenuate più o meno indipendentemente, per cui la diversità in frequenza è ancora presente.
Incertezza di canale
Abbiamo finora assunto la perfetta conoscenza del canale, cosicché potesse essere fatta, al ricevitore, una rivelazione coerente.
Nei canali che variano velocemente può non essere facile stimare accuratamente fase e ampiezza dei guadagni prima che essi cambino.
In questo caso, bisogna capire l'impatto della stima degli errori nel canale sulla performance.
In alcune situazioni, la rivelazione non-coerente, che non richiede la stima di canale, può essere la scelta preferita.
Nel paragrafo 1.1.1 abbiamo già parlato di una semplice rivelazione non-coerente per canali con fading senza diversità, adesso vedremo il caso di canali con fading con diversità.
Quando abbiamo paragonato la rivelazione coerente e non-coerente per canali senza diversità, la differenza era relativamente piccola.
Un problema importante è vedere che cosa accade a quella differenza quando aumenta il numero L dei cammini in diversità.
La risposta a questo problema dipende dalla diversità dello scenario.
Osservando la situazione in cui la incertezza di canale ha più impatto, cioè il DS spread-spectrum su canali con diversità di frequenza, è interessante paragonare la performance della rivelazione coerente e non coerente come funzione del numero dei rami in diversità.
Questo è rappresentato nelle figure 1.10 e 1.11.
Per L=1, il gap tra le performance dei due schemi è piccolo, ed è in entrambi i casi pessimo a causa della assenza di diversità.
Come L aumenta, la performance della rivelazione coerente migliora in maniera monotona e approssima la performance di un canale AWGN.
Al contrario, la performance di una rivelazione non-coerente, prima migliora con L, ma dopo, aumentando ancora L, peggiora.
|
|
|
Figura 1.10 - Confronto tra la probabilità di errore della rivelazione coerente e non coerente in funzione del numero di prese (SNR = 10dB). |
|
|
|
Figura 1.11 - Confronto tra la probabilità di errore della rivelazione coerente e non coerente in funzione del numero di prese (SNR = 15dB). |
Il miglioramento iniziale proviene dal guadagno in diversità.
C'è poi un peggioramento rispetto al guadagno in diversità.
Infatti quando L diventa molto grande, il SNR per ciascun cammino diventa molto piccolo e una rivelazione non-coerente non può efficacemente venire sfruttata per ottenere una affidabile diversità.
Questo porta, in definitiva, ad una degradazione della performance.
Infatti, si può dimostrare che per ![]() la probabilità di
errore tende ad
la probabilità di
errore tende ad ![]() .
.
Stima di canale
La significativa differenza di performance, tra la rivelazione coerente e non-coerente, quando il numero di rami è grande, suggerisce l'importanza della conoscenza del canale nei sistemi a larga banda.
Quando si assume la perfetta conoscenza del canale e si analizza la performance del ricevitore coerente, in pratica si opera una stima del canale.
È perciò importante capire l'impatto degli errori di misura di canale sulla performance del rivelatore coerente.
Nella rivelazione dei dati, la sequenza trasmessa è una delle possibili sequenze che rappresentano i dati.
Nella stima di canale, si assume che la sequenza trasmessa sia nota al ricevitore.
Possiamo pensare ad uno schema in cui una sequenza nota, chiamata pilota, venga trasmessa e usata per la stima di canale.
Oppure possiamo pensare ad uno schema in cui vengono utilizzate decisioni feedback basate su simboli precedentemente rivelati.
Per una certa quantità di potenza in
trasmissione deputata alla stima del canale, l'efficacia della performance di
rivelazione dipende dal parametro chiave ![]() , cioè il rapporto SNR ricevuto
per tempo di coerenza e per diversità di cammino.
, cioè il rapporto SNR ricevuto
per tempo di coerenza e per diversità di cammino.
Se ![]() , allora la performance di rivelazione è prossima a quella
coerente, se invece
, allora la performance di rivelazione è prossima a quella
coerente, se invece ![]() , allora è impossibile una effettiva rivelazione.
, allora è impossibile una effettiva rivelazione.
 |
| Appunti su: appuntimania, |
|
| Appunti Diritto |  |
| Tesine Inglese |  |
| Lezioni computer |  |