 |
|
| Appunti universita |
|
 |
|
| Appunti universita |
|
| Visite: 1944 | Gradito: |
Leggi anche appunti:Nichel solfatoNICHEL SOLFATO Il nichel, sia in forma metallica che sottoforma di ossido Il teatro grecoIl teatro greco Non ci sono molte testimonianze è quindi molto difficile DesignDesign Con design (industrial design) si indica l'insieme delle attività |
 |
 |
ESAME DI MATURITA'
RINCHIUSI NELLO STRANO ANELLO
(senza aver bevuto un tè dal Cappellaio e dalla Lepre Marzolina!)
![]()

Non c'è bisogno di sognare di essere Alice.
Non c'è bisogno di seguire un coniglio bianco col panciotto per cadere in un mondo che metta a dura prova le nostre certezze e quelle del nostro sistema di ragionamento.
Non serve ascoltare un simpatico discorso tra la Lepre Marzolina e il Cappellaio Matto all'ora del tè per aggrottare la fronte, roteare velocemente entrambe le pupille e tentare, dopo un intenso sospiro, di riprendere il filo del discorso che sembra essere scappato chissà dove.
Il mondo di Alice è il nostro: anche le pareti della nostra realtà sono intinte di sfumature d'assurdo. Il paradosso è una costante della nostra vita.
Cos'è un paradosso? Una smagliatura nella nostra conoscenza? Un infernale prodotto della nostra mente che si diverte a mettere in discussione la realtà, o ciò che "crediamo" tale? E' un lusso per le persone con elevato senso umoristico e che si limitano a divertirsi con questi "giochi", o un antico, ma altrettanto sofisticato, "navigatore satellitare" che ci consiglia con poca invadenza quale strada percorrere per migliorare i nostri strumenti di analisi del mondo? Un mero esercizio per vivacizzare l'intelletto o un monito degli déi (come scrive Wittgenstein nelle Osservazioni sopra i fondamenti della matematica) perché si agisca senza riflettere?
I paradossi sono definiti da Odifreddi come "gli argomenti che imbarazzano il pensiero, sorprendenti perché poco probabili, ma molto credibili, oppure molto probabili, ma poco credibili". Il nostro pensiero ne è imbarazzato, eppure ne è segretamente attratto: così, per seguire quel filo che sfugge, si sale, poi si scende, ma ci si ritrova stranamente prima più giù e poi più su.
A sinistra, Salita
e discesa, di M. C. Escher (litografia, 1960) ; Sotto,
un particolare
Altre
volte, pur salendo e scendendo vari scalini, ci si ritrova inaspettatamente al
punto di partenza, come se i gradini fossero quelli dell'opera di Escher
"Salita e discesa".


Questo è il fenomeno che Douglas R. Hofstadter in "Gödel, Escher, Bach: un'Eterna Ghirlanda Brillante" definisce Strano Anello.
Gödel ne scoprì uno persino nella matematica e cosa più intrigante, sembra essere proprio la traduzione in termini matematici di uno dei più antichi paradossi filosofici: il paradosso di Epimenide o del mentitore.
Questi strani anelli quindi, o paradossi, sembrano essere dappertutto e soprattutto accompagnano da sempre gli uomini! Alcuni, come Russell, hanno tentato di estromettere questa invadente presenza che si nasconde bene per poi far capolino nei momenti meno opportuni. Al contrario, Lewis Carroll, il 'padre'di Alice e di quel "meraviglioso" mondo, governato da regole incomprensibili e paradossali perché distanti da quelle cui il nostro senso comune ci ha abituato, era piuttosto occupato a bearsi dell'esistenza di tali anelli. Il mondo che l'autore inglese descrive non solo è di per sé un paradosso, ma lo stesso linguaggio utilizzato dai suoi abitanti per esprimersi è un nonsense, che oltre a far sorridere, lascia intravedere quale immenso potere abbiamo sulle parole:
«Quando io uso una parola» -disse Humpty Dumpty ad Alice- «quella significa ciò che io voglio che significhi, né più, né meno».
I poeti moderni sembrano aver raccolto tale suggerimento! Infatti, la poesia moderna va oltre la concezione della parola che indichi concretamente l'oggetto al quale si riferisce nel nostro immaginario comune.
Wittgenstein ne sembrava invece tormentato e dedicò i suoi studi a un'attività di analisi del linguaggio per distinguere quello dotato di senso, da quello senza senso.
Divertente, scomoda, accattivante, preziosa è l'esperienza di restare rinchiusi in uno strano anello che può "paradossalmente"aprire, allargare gli orizzonti del pensiero.
E' in questo modo che sognare di essere Alice diventa inutile, perché all'improvviso ci si sente "Alice".
. E riecheggiano nella mente le parole di una regina:
«Con l'esercizio puoi imparare a credere anche alle cose impossibili» .
SENZA CHIAVE
Non sono pochi gli "strani anelli"in cui, in passato, sono rimasti rinchiusi filosofi e pensatori.
I Greci li chiamavano paralogismi, «contro la logica»; per i medioevali si trattava di insolubilia, «problemi senza soluzione»; i moderni hanno imparato a chiamarli antinomie, «contro le regole». Da sempre sono comunque paradossi: «contro l'opinione comune».
Sorge spontanea una domanda: i nostri "antenati", più o meno vicini, erano stolti o è veramente così semplice mettere in difficoltà il nostro sistema di ragionamento?
Proviamo a conoscere queste "prigioni della mente", cerchiamo di trovare la chiave che le apre e a uscirne sani e salvi!
Il paradosso del mentitore
Il più antico paradosso si ritiene essere il paradosso del mentitore, che la tradizione attribuisce ad Epimenide, un saggio greco vissuto all'inizio del VI secolo a.C., ma che quasi sicuramente risale a Eububilde di Mileto (IV secolo a.C.). Oggi non disponiamo della formulazione originaria, ma di una serie di versioni così ampia, che ci risulta difficile determinare se esse abbiano avuto come punto di partenza la medesima fonte. Eccone una descrizione sintetica:
Epimenide cretese diceva che tutti i cretesi erano bugiardi. Ma allora: diceva il vero o il falso? Se diceva il vero, mentiva asserendo che tutti i cretesi erano bugiardi (egli stesso era, infatti, cretese). Se diceva il falso, non mentiva, come cretese, quindi diceva il vero.
Da ciò l'antinomia, senza soluzione: se diceva il vero, mentiva; se mentiva, diceva il vero.
Il dilemma del coccodrillo
Diogene Laerzio (II secolo d.C.) diffuse un'altra antinomia.
Un coccodrillo, dopo aver rubato un bimbo, promise alla madre di renderglielo, a patto che ella avesse indovinato la sua intenzione di restituirglielo o meno. La madre rispose che il coccodrillo non gliel'avrebbe restituito, gettando il coccodrillo in un dilemma insolubile. Infatti, se non glielo avesse restituito avrebbe fatto avverare la risposta della madre e, per rispettare il patto, avrebbe dovuto procedere alla consegna del bimbo alla madre. Viceversa, se glielo avesse restituito, avrebbe reso falsa la risposta della madre e, in base al patto non avrebbe dovuto consegnare il piccolo.
In entrambi i casi, il coccodrillo si sarebbe trovato in una posizione imbarazzante e contraddittoria.
Il paradosso del barbiere
Tale paradosso è uno dei più famosi della filosofia matematica moderna. Fu formulato da Bertrand Russell, filosofo e matematico inglese, nel . Il concetto può essere espresso non formalmente così:
In un villaggio c'è un unico barbiere. Il barbiere rade tutti (e soli) gli uomini che non si radono da soli. Il barbiere è ben sbarbato. Il barbiere rade se stesso?
Anche in questo caso si possono formulare due ipotesi: se il barbiere rade se stesso, allora per definizione il barbiere non rade se stesso. Se il barbiere non rade se stesso allora, giacché il barbiere rade tutti quelli che non si radono da soli, il barbiere rade se stesso.
Si ottiene in entrambi i casi ancora una contraddizione.
Questi tre esempi sembrano indicare uno stesso colpevole: la presenza di uno strano anello. Questa versione "ampliata" di Epimenide ricorda Mani che disegnano di Escher:
L'enunciato che segue è falso
L'enunciato precedente è vero
Congiuntamente questi enunciati danno lo stesso risultato del paradosso di Epimenide; eppure, separatamente, sono enunciati innocui. Non è possibile addossare la "colpa"di questo strano anello all'uno o all'altro dei due enunciati, ma solo al modo in cui essi si "riferiscono"l'uno all'altro. Questo fenomeno è detto AUTOREFERENZA.
|
Mani che disegnano, di M.C. Escher (litografia, 1948) La mano sinistra disegna la mano destra, mentre contemporaneamente la mano destra disegna la mano sinistra . Quale mano disegna realmente l'altra? |
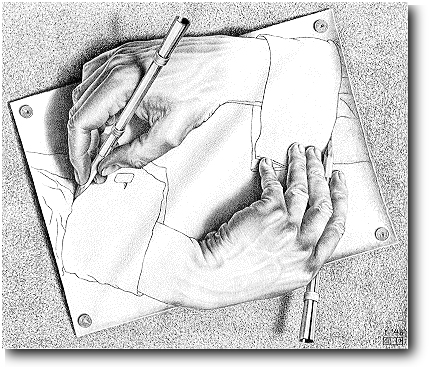
Analogamente, le singole aree di Salita e discesa (vedi prefazione) sono del tutto coerenti; è soltanto il modo in cui sono messe insieme che crea un'impossibilità.
L'unica "chiave" è dunque escludere la possibilità dell'autoreferenza?
NEUTRALIZZARE IL NEMICO
Il paradosso del barbiere può essere generalizzato; ma, proprio da tale generalizzazione Russell arrivò ad un'antinomia che mise in crisi l'intera teoria matematica del Novecento e progressi che sembravano essere stati fatti in passato.
Proviamo a trattare il paradosso del barbiere con un approccio insiemistico.
Siamo di fronte a due insiemi distinti:
A: gli uomini che si radono da soli
B: gli uomini che si fanno radere dal barbiere
Il problema è collocare il barbiere in uno dei due insiemi, poiché, come analizzato in precedenza, la sua inclusione in uno dei due insiemi creerebbe una contraddizione.
Da qui Russell formulò il seguente problema: "Un insieme può essere o no elemento di se stesso?". Ad esempio, l'insieme di tutti i libri di una biblioteca non è elemento di se stesso. L'insieme dei trichechi non è un tricheco, l'insieme che contiene Giovanna d'Arco non è Giovanna d'Arco e così via. Da questo punto di vista, la maggior parte degli insiemi può essere considerata di "Ordinaria Amministrazione". Tuttavia, esistono alcuni insiemi ad "Auto-Ingerimento", che contengono se stessi come elementi. Un esempio: l'insieme di tutti gli insiemi con più di venti elementi è elemento di se stesso.
Se si pensa, invece, all'insieme di tutti gli insiemi che non sono elementi di se stessi? Esso è o no elemento di se stesso? È evidente la somiglianza del problema col paradosso del barbiere. Se l'insieme (detto 'I' per comodità) non fosse elemento di se stesso, allora dovrebbe essere elemento di se stesso. E, analogamente, se lo fosse, non dovrebbe esserlo. La posizione di 'I' rispetto a se stesso genera ad ogni modo una contraddizione.
Che cosa è "I" allora?
La questione rimase sospesa per qualche anno, tempo necessario a Bertrand Russell e Alfred North Whitehead per elaborare un sistema che potesse finalmente estromettere dalla teoria degli insiemi, dalla logica e dall'aritmetica qualsiasi genere di "strano anello": in questo consisteva la gigantesca impresa dei Principia Mathematica.
L'"arma" essenziale era rappresentata dalla Teoria dei Tipi.
L'idea era essenzialmente questa: un insieme del "tipo"più basso poteva avere come elementi solo "oggetti", non insiemi.
Un insieme del tipo successivo poteva contenere solo oggetti o insiemi del tipo più basso. In generale, un insieme di un dato tipo poteva contenere solo oggetti o insiemi del tipo inferiore.
Chiaramente, nessun insieme poteva contenere se stesso, poiché sarebbe dovuto appartenere a un tipo superiore al proprio.
In un sistema del genere esistono soltanto insiemi di "Ordinaria Amministrazione" e il nostro insieme "I" non viene nemmeno più considerato tale, visto che non appartiene ad alcun tipo definito.
Questa teoria dei tipi, quindi, spazza via qualsiasi paradosso all'interno della teoria degli insiemi, ma solo a costo di introdurre una gerarchia alquanto artificiale e di proibire la formazione di insiemi con certe caratteristiche, come l'insieme "I", che la nostra intuizione spontaneamente ci suggerisce.
Per chi era interessato solo alla teoria degli insiemi, ciò poteva anche bastare - "chi si accontenta, gode!"- recita un proverbio, che poteva certo valere per quanti erano interessati a eliminare i paradossi in generale.
Cosa ne sarebbe stato di tutti quei paradossi racchiusi nel nostro linguaggio?
Si sarebbe dovuto procedere nel verso di una "gerarchizzazione" alla cui base vi sarebbe stato un linguaggio-oggetto. Se fosse stato inventato, in esso sarebbe possibile riferirsi soltanto a un dominio specifico e non ad aspetti del linguaggio-oggetto medesimo, come regole grammaticali o enunciati particolari; per parlare di questi, vi sarebbero un metalinguaggio, e poi un meta-metalinguaggio che discute del metalinguaggio, e ancora un meta - meta - metalinguaggio e così via . Quanti enunciati dovremmo eliminare, perché non appartenenti a un punto preciso della gerarchia e perciò privi di significato!
Per il nostro linguaggio, che è un aspetto onnipresente della nostra vita, una stratificazione del genere non può che essere considerata assurda.
LA SPERANZA DI HILBERT
Dopo il 1913, anno della pubblicazione dei Principia Mathematica, largamente ammirata da tutti i matematici, nessuno aveva la completa certezza che tutta la matematica fosse realmente contenuta nei metodi indicati da Russell e da Whitehead, e che, almeno, i metodi esposti fossero coerenti fra loro.
Era veramente sicuro che mai nessun matematico avrebbe potuto ottenere risultati contraddittori seguendo i metodi di Russell e di Whitehead?
L'insigne matematico tedesco David Hilbert era turbato da questo problema e lanciò una sfida a tutti i matematici: dimostrare rigorosamente, magari seguendo proprio i metodi indicati da Russell e Whitehead, che il sistema definito nei Principia Mathematica era
v Coerente: non-contraddittorio
v Completo: tale cioè che ogni enunciato vero dell'aritmetica potesse essere derivato all'interno della struttura predisposta nei Principia Mathematica.
Era un compito arduo, ed era anche criticabile, poiché per certi versi appariva circolare: com'è possibile giustificare un metodo di ragionamento secondo quello stesso metodo di ragionamento? E' un po' come sollevarsi reggendosi ai tiranti dei propri stivali.
Hilbert era pienamente cosciente di questo dilemma, ovviamente; perciò sperava di trovare un numero ristretto di metodi, accettati da tutti i matematici, per dimostrare la coerenza o la completezza di un sistema. In questo modo i matematici, seppur parzialmente, avrebbero potuto sollevarsi reggendosi ai tiranti dei propri stivali!
Questo obiettivo, piuttosto stravagante, occupò le menti dei più grandi matematici del mondo durante i primi trent'anni del XX secolo .
GÖDEL: LA "PICCOLA PESTE"
Nel 1931, il matematico, logico e filosofo di origine boema, Kurt Gödel pubblicò, all'età di soli venticinque anni, un articolo che demolì completamente il programma di Hilbert.
Quell'articolo non solo rivelò la presenza di "buchi"irreparabili nel sistema assiomatico di Russell e di Whitehead, ma, più in generale, evidenziò l'impossibilità dell'esistenza di un qualche sistema assiomatico in grado di produrre tutte le verità aritmetiche, a meno che il sistema in questione non fosse incoerente! Infine, rese vana anche la speranza di dimostrare la coerenza di un sistema come quello presentato nei Principia Mathematica. Se fosse possibile trovare una dimostrazione del genere usando solo metodi disponibili entro i Principia Mathematica, allora, e questa è una delle conseguenze del lavoro di Gödel che disorientano maggiormente, gli stessi Principia Mathematica sarebbero incoerenti!
La cosa ancora più sorprendente è che con la dimostrazione di questo Teorema di Incompletezza, Gödel introdusse nei Principia Mathematica qualcosa di analogo proprio al paradosso di Epimenide! Gödel si concentrò sui numeri naturali, quindi sulla sola aritmetica. Egli attuò una codifica, cioè una traduzione numerica degli enunciati; il sistema formale così ottenuto permette a un enunciato non solo di parlare dei numeri naturali, ma di parlare di altri enunciati, e in particolare di se stesso. Ogni enunciato può essere riferito ai numeri o ad altri enunciati. In questo modo violiamo la Teoria dei Tipi!
Consideriamo l'enunciato G di Gödel, o meglio, una sua probabile riformulazione:
Questo enunciato dell'aritmetica non ammette alcuna dimostrazione nel sistema dei Principia Mathematica (PM)
G è un teorema dei PM? Se sì, allora deve
asserire una verità. Ma che cosa asserisce in effetti G? Asserisce di non
essere un teorema. Quindi, se fosse un teorema, se ne potrebbe dedurre che non
è un teorema: questa è una contraddizione.
E se G non fosse un teorema? Ciò è accettabile, perché non porta a una
contraddizione. Ma G asserisce proprio questo, cioè di non essere un teorema;
quindi G asserisce una verità. E poiché G non è un teorema, vi è (almeno) una
verità che non è un teorema dei PM.
Se i Principia Mathematica sono stati la prima vittima di questo colpo, non furono certo l'ultima! Infatti, il teorema di Gödel asserisce che:
Tutte le assiomatizzazioni coerenti dell'aritmetica
contengono proposizioni indecidibili.
In qualsiasi sistema coerente esiste una proposizione tale che non è possibile dimostrare né la sua affermazione né la sua negazione all'interno del sistema.
* Allo stesso modo, si può concludere che in ogni sistema coerente non è possibile provare la sua coerenza all'interno del sistema stesso.
NEL PAESE DELLE MERAVIGLIE
Il nostro percorso attraverso la storia dei paradossi ha svelato, senza possibilità di fraintendimenti, che neanche una creazione di sistemi artificiosi e rigidi po' contenere la potenza di uno "strano anello" inoltre, tali sistemi avrebbero ingabbiato troppo le stranezze e le bizzarrie che rendono interessanti la matematica e soprattutto la vita!
Il nostro mondo è il "Paese delle Meraviglie": il nonsense che pervade le avventure di Alice, il continuo "volteggiare"da un paradosso all'altro senza possibilità di fermarsi, fino a credere di poter perdere le coordinate del mondo e di tutto ciò che ne fa parte, talvolta persino di se stessi, sono condizioni che combaciano perfettamente con l'esperienza del mondo che tutti i giorni facciamo. Il che non rende, però, necessariamente disperata l'esistenza.
Insegna il Re di Cuori: "Se un senso non c'è, questo ci evita un sacco di guai, perché non dobbiamo cercare di trovarlo"
CON GLI OCCHI E LE ORECCHIE DI ALICE
Charles Lutwidge Dodgson, scrittore, matematico, logico e fotografo britannico, noto con lo pseudonimo di Lewis Carroll è l'autore dei due romanzi più celebri di tutta la letteratura nonsense cui in precedenza si è già fatto riferimento e di cui sono state citate alcune frasi. Il famoso "Alice nel Paese delle Meraviglie" (Alice's Adventures in Wonderland) e il suo seguito, meno rinomato "Attraverso lo Specchio - e quel che Alice vi trovò" (titolo tradotto di Through the Looking-Glass, and What Alice Found There) ci propongono episodi fantastici e divertenti paradossali, appunto.
 Dal
coniglio bianco, con tanto di panciotto, orologio e guanti, che corre
velocemente, trascinandosi dietro la curiosa Alice, alla Regina di Cuori con la
mania di far decapitare chiunque, e che istruisce un processo perché qualcuno
le ha rubato i pasticcini, dai giudici di tale processo che scrivono sulle loro
lavagnette il proprio nome per paura di dimenticarlo, sino al Re di Cuori che
pretende dagli stessi un verdetto prima di ascoltare i testimoni: tutto sembra
confermare, agli occhi di Alice, le parole del gatto del Cheshire.
Dal
coniglio bianco, con tanto di panciotto, orologio e guanti, che corre
velocemente, trascinandosi dietro la curiosa Alice, alla Regina di Cuori con la
mania di far decapitare chiunque, e che istruisce un processo perché qualcuno
le ha rubato i pasticcini, dai giudici di tale processo che scrivono sulle loro
lavagnette il proprio nome per paura di dimenticarlo, sino al Re di Cuori che
pretende dagli stessi un verdetto prima di ascoltare i testimoni: tutto sembra
confermare, agli occhi di Alice, le parole del gatto del Cheshire.
|
Ma io non voglio andare tra i matti! - osservò Alice. Oh non puoi farne a meno, - disse il Gatto, - qui siamo tutti matti. Io sono matto, tu sei matta. Come sai che io sia matta? - domandò Alice. Tu sei matta - rispose il Gatto - altrimenti non saresti venuta qui. |
Una "maratonda"(maratona in tondo, in cui nessuno mai arriverà prima di un altro!) che "cominciò domani e l'altro ieri finirà", un tè con il Cappellaio Matto e la Lepre Marzolina, una partita a croquet con fenicotteri e ricci, sono solo alcune delle avventure che stravolgono i ragionamenti di Alice.
In "Attraverso lo Specchio" la bambina sente parlare di "memoria che lavora in due sensi" (memoria del passato e del futuro), è costretta a camminare all'indietro per procedere in avanti, e mangia una fetta di torta prima di tagliarla!
Oltre la fantasia si nascondono meravigliosi esempi di giochi logici e di parole che evidenziano l'assoluta arbitrarietà di uno degli strumenti di comunicazione nella nostra storia: il linguaggio.
Alice, per esempio, dopo aver pianto molto, trovatasi poi immersa nel "lago di lacrime", si imbatte in un gruppetto di animali che raggiunge poi a riva; tutti quanti sono bagnati e infreddoliti e il topo presente nella comitiva si propone di asciugarli raccontando una vicenda di Guglielmo il Conquistatore, la storia più "seccante" che conosceva.
La doppia accezione di "seccante" - "che asciuga" oppure "noioso" - provoca un'incongruenza all'interno della vicenda, giacché tutti quanti rimangono bagnati fradici!
Alice addentò un boccone e si chiese ansiosa: 'Come divento, come divento?'. Si teneva la mano sulla testa per sentire se la sua statura cresceva, ma restò molto sorpresa quando si accorse che era sempre la stessa.
Se ci si mette la mano sulla testa, non si può capire se si sta crescendo o rimpicciolendo (salvo che non sia il solo collo a crescere).
'Non
va' disse il Bruco.
'Forse non proprio tutto, ' rispose timida Alice. 'Qualche
parola non m'è venuta giusta.'
'Era tutto sbagliato, dal principio alla fine, ' disse il Bruco con
tono convinto.
Seguì un lungo silenzio, ancora più penoso.
Non si può recitare una poesia 'in modo sbagliato dal principio alla fine', poiché in tal caso non si può più neanche affermare che si sta recitando quella poesia.
'Allora
dimmi subito quello che credi' riprese la Lepre.
'Come volete' rispose in fretta Alice. 'Vi dico quello che
credo perché io quello che credo dico è la stessa cosa.'
'Non è per niente la stessa cosa!' esclamò il Cappellaio. 'Vorresti
forse sostenere che la frase 'vedo quello che mangio' ha lo stesso
significato di 'mangio quello che vedo'?'
Il Cappellaio Matto presuppone la totale indipendenza di significato e parola.
'Questa
marmellata è ottima' disse la Regina.
'Non ne dubito, comunque oggi non mi va.'
'Non potresti averla neanche se ti andasse' precisò la Regina.
'Abbiamo una regola: marmellata domani e marmellata ieri, ma mai
marmellata oggi.'
'Ma qualche volta ci deve essere il giorno della 'marmellata oggi''
obiettò Alice.
'No, no, impossibile' disse la Regina. 'La marmellata è prevista
ogni altro giorno, e oggi, sai, non è nessun altro giorno, lo vedi da te.'
'Non la seguo' rispose Alice, 'mi sembra terribilmente confuso'.
Questo esempio dimostra
che il termine 'oggi', nonostante le analogie, non ha funzione di
data.
Nel capitolo VII dello Specchio, il Re Bianco chiede ad Alice se vede qualcuno sulla strada, lei gli risponde di no, e il Re la invidia per la sua buona vista, che riesce a vedere Nessuno: lui a mala pena riesce a vedere qualcuno. Quando poi il Messaggero arriva, il Re gli chiede se ha sorpassato qualcuno lungo la via, lui risponde di no, e il Re conferma che anche Alice ha visto Nessuno, e che dunque Nessuno viaggia più lentamente. Il Messaggero si offende, dicendo che invece nessuno viaggia più veloce, ma il Re ribatte che se così fosse, Nessuno sarebbe arrivato prima.
La fallacia consiste nell'utilizzare "nessuno" alla stregua degli altri pronomi indefiniti, come "tutti" e "qualcuno".
"Prendi più tè"- disse la Lepre Marzolina.
"Non ne ho ancora preso niente, non posso prenderne di più" - osservò Alice.
"Vuoi dire non puoi prenderne di meno. E' facile prendere più di niente" - rispose la Lepre.
"Quanti anni hai detto di avere?"- le chiese Humpty Dumpty.
"Sette e mezzo" - disse Alice.
"Sbagliato! Non l'hai mai detto!".
"Credevo volessi dire quanti anni ho".
"Se avessi voluto dirlo, l'avrei detto" - osservò Humty Dumpty.
Questi "equivoci"linguistici mostrano, ancora una volta, quanto sia vicina a noi, in ogni istante, la possibilità di ascoltare discorsi sulla falsa riga di quelli del Mad Tea Party dal Cappellaio e dalla Lepre.
Da cosa dipende tutto ciò? E' quello di cui si occuparono molti filosofi della prima metà del Novecento, di cui ricordiamo Wittgenstein, le cui opere sono a tutt'oggi oggetto di studio e di riflessione.
LINGUAGGIO: TORMENTO E DELIZIA
Ludwing Wittgenstein, nato a Vienna nel 1889, fu allievo all'università di Cambridge di Russell, il quale, affascinato dal talento del suo giovane allievo scriveva nel 1912: «Fra cinque anni credo di dover interrompere l'insegnamento; Wittgenstein può allora occupare il mio posto.». Quando, nel 1922, Wittgenstein pubblicò il celebre Tractatus logico - philisophicus, Russell ne curò l'introduzione.
Il tale opera Wittgenstein elaborò la teoria del linguaggio come raffigurazione.
E' la concezione secondo cui il linguaggio mostra e indica i fatti. A tal proposito, si deve parlare di una corrispondenza tra le proposizioni e i fatti del mondo, cioè, in termini tecnici, di "isomorfismo" tra linguaggio e realtà.
Il linguaggio "rappresenta" la realtà, ne costituisce l'immagine come un oggetto reale, tridimensionale, può essere rappresentato sulla carta attraverso una "proiezione" geometrica bidimensionale; così una situazione reale può essere "raffigurata" da un altro fatto, la "proposizione".
Tra "fatto" e "immagine linguistica" esiste un'identità strutturale: gli elementi del fatto corrispondono agli elementi dell'immagine, e la connessione dei primi è raffigurata dalla corrispondenza dei secondi.
Il Tractatus afferma che "il mondo è la totalità dei fatti, non delle cose".
Le cose sono le realtà più semplici, non ulteriormente scomponibili, sono "ciò che sussiste indipendentemente da ciò che accade"; i fatti sono "ciò che accade" e sono determinati dalle relazioni tra le cose.
Le proposizioni sono vere se possono essere sottoposte al criterio di verificabilità, in altre parole se l'empiria è in grado di dimostrare che esse corrispondono a qualche aspetto del reale.
Il Tractatus si chiude con la celebre frase: "Su ciò di cui non si può parlare, si deve tacere". Il linguaggio, quindi, è soltanto quello della scienza. (E' facile trovare delle somiglianze con le teorie di Russell)
Eppure, oltre la scienza c'è l'uomo, ci sono i suoi desideri, le emozioni
La "svolta", nella teoria di Wittgenstein, fu segnata nel 1953, quando il filosofo pubblicò l'opera intitolata Ricerche filosofiche, frutto di tanti anni di osservazione e di studi sviluppati dagli anni Trenta.
Passando vicino a un campo da calcio dov'era in corso una partita, si accorse che, anche nel linguaggio, non facciamo altro che giocare con le parole. La prima conseguenza è che, così come non c'è un unico gioco universale, non c'è neppure un linguaggio universale.
«Il significato di una parola - dice il filosofo - è il suo uso nel linguaggio»; ciò vuol dire che le parole non hanno in sé, incorporato, un senso immutabile ed eterno, riflesso delle essenze delle cose, ma, al contrario, desumono il loro significato dai contesti d'uso. Nelle Ricerche filosofiche troviamo questa efficace metafora:
«Pensa agli strumenti - scrive Wittgenstein - che si trovano in una cassetta di utensili: c'è un martello, una tenaglia, una sega, un cacciavite, un metro, un pentolino per la colla, la colla, chiodi e viti. - Quanto differenti sono le funzioni di questi oggetti, tanto differenti sono le funzioni delle parole».
Il linguaggio è un insieme di "giochi linguistici", le cui regole variano da situazione a situazione. Il senso di un enunciato è legato non più al modo in cui può essere verificato, ma da come si sposa col contesto in cui è usato.
E' insensato un enunciato che non rispetta le regole del gioco!
 Tale posizione
potrebbe coincidere con quella di Humpty Dumpty:
Tale posizione
potrebbe coincidere con quella di Humpty Dumpty:
|
Quando io uso una parola, - disse Humpty Dumpty in tono d'alterigia, - essa significa ciò che appunto voglio che significhi: né più né meno. Si tratta di sapere, - disse Alice, - se voi potete dare alle parole tanti diversi significati. Si tratta di sapere, - disse Humpty Dumpty, - chi ha da essere il padrone Questo è tutto. |
Il suggerimento dell'Uovo seduto sul muretto può coincidere con la filosofia di Wittgenstein solo nel limite in cui il linguaggio non diventi un fatto privato: le regole non si possono seguire privatamente!
Coloro che invece "giocano" con le parole sono senza dubbio i poeti. Le parole, i suoni, assumono per ognuno una funzione diversa e si caricano di significato a discrezione dell'autore
CHIEDERE O NON CHIEDERE LA PAROLA?
Pensando ai giochi di parole nella poesia è immediata l'associazione ai poeti futuristi. Con il Manifesto tecnico della letteratura futurista, scritto da Filippo Tommaso Marinetti nel 1912, diventa chiara la volontà di rottura dei poeti con le forme e le esperienze letterarie del passato.
Il futurismo sostituisce a qualsiasi forma che esprimesse causalità e consequenzialità, i pilastri su cui si fonda la logicità del pensiero, una forma più sintetica e abbreviata: l'analogia.
L'analogia accosta fra loro realtà diverse e lontane, non per un passaggio di giustificazioni logiche, ma attraverso un semplice accostamento, che suggerisce un rapporto di somiglianza fantastica.
Marinetti scriveva: «Gli scrittori si sono abbandonati finora all'analogia immediata. Hanno paragonato l'animale all'uomo o ad un altro animale, il che equivale ancora, press' a poco, a una specie di fotografia. [] L'analogia non è altro che l'amore profondo che collega le cose distanti, apparentemente diverse e ostili».
La parola perde così la funzione, che le era attribuita della letteratura tradizionale, di indicare concretamente l'oggetto al quale si riferisce; il suo significato diventa polisemico, allusivo, evocatore, permettendo di cogliere la vastità e lo spessore del reale, al di là di ogni sua rappresentazione in termini puramente fenomenici.
Si afferma definitivamente il concetto della parola come segno autonomo e arbitrario rispetto ai contenuti della realtà rappresentata.
Ciò comporta anche una distruzione della sintassi tradizionale: sono aboliti i segni d'interpunzione, i tempi verbali sono sostituiti dall'uso dell'infinito che indica il senso della durata e della continuità.
A tale distruzione si sostituisce la teoria delle "parole in libertà", che consiste nel disporre i sostantivi a caso, come nascono. Notevole importanza assume la forma grafica stessa delle parole, che rileva effetti particolari, insieme all'immagine mentale che può produrre, ma anche come segno concretamente visibile, destinato a sua volta a suggerire impressioni acustiche o tattili.
Ungaretti, ricollegandosi alla lezione del Simbolismo, portò alle estreme conseguenze il procedimento dell'analogia. Riprese in ciò anche alcuni presupposti della poetica di Marinetti, di cui però respingeva il dinamismo meccanicistico. Scriveva, infatti: «Se il carattere dell'Ottocento era quello di stabilire legami a furia di rotaie e di ponti e di pali e di carbone e di fumo - il poeta d'oggi cercherà dunque di mettere a contatto immagini lontane, senza fili. Dalla memoria all'innocenza, quale lontananza da varcare; ma in un baleno».
La poesia assume così un valore religioso e metafisico, perché diventa il luogo d'incontro tra storia e assoluto, individuale e universale.
Si passa perciò a quello che è un vero e proprio culto della parola, che è caricata al massimo di tensione espressiva. La parola isolata nel bianco tipografico della pagina è la parola carica di senso che il poeta cerca di far uscire dal silenzio della vita per esprimere l'assoluto. Si esprime così la fiducia nel potere della poesia quale rivelazione della verità per mezzo della ricerca sulle parole. La parola assume il valore di un'improvvisa e folgorante illuminazione: essa s'identifica con l'attimo in cui, attraverso l'immediatezza del rapporto analogico, la poesia sfiora la totalità e la pienezza dell'essere.
M'illumino
d'immenso
Il testo riportato è da considerare come l'esito estremo cui potesse giungere la ricerca poetica ungarettiana, nella sua ansia di un'estrema riduzione e semplificazione, che, arrestandosi alle soglie del silenzio, cerca di raggiungere l'assoluto.
Per Montale, invece, tra l'uomo e l'assoluto c'è una realtà ineliminabile.
Di qui, il diverso valore che, rispetto a Ungaretti, assume la parola nella ricerca poetica montaliana. La parola non può aspirare a raggiungere direttamente l'assoluto, isolando la sua pronuncia nel silenzio, ma deve prima confrontarsi con il reale, una barriera nella quale resta inevitabilmente impigliata.
Non chiederci la parola che squadri da ogni lato l'animo nostro informe []
Non domandarci la formula che mondi possa aprirti []
Mentre Ungaretti accosta fra loro realtà antitetiche e lontanissime, Montale non allude o elude, ma indica con precisione oggetti definiti e concreti, nei quali trovano espressione e definizione anche i concetti e i sentimenti più astratti. E' questa la poetica del "correlativo oggettivo", di cui "Spesso il male di vivere ho incontrato" costituisce un valido esempio:
Spesso il male
di vivere ho incontrato:
era il rivo strozzato che gorgoglia,
era l'incartocciarsi della foglia
riarsa, era il cavallo stramazzato.
Bene non seppi, fuori
del prodigio
che schiude la divina Indifferenza:
era la statua nella sonnolenza
del meriggio, e la nuvola, e il falco alto
levato.
Naturalmente, la ricerca a tutto ciò che rende il nostro mondo lo stesso in cui cade Alice non può esaurirsi con questo lavoro.
Come affermato nella prefazione, ci vuole un po' di esercizio per credere alle cose impossibili
BIBLIOGRAFIA
Douglas R. Hofstadter "Gödel, Escher, Bach: un'Eterna Ghirlanda Brillante"
Lewis Carroll "Alice nel paese delle Meraviglie"; "Attraverso lo Specchio - e quel che Alice vi trovò"
G. Baldi - S. Giusso - M. Razetti - G. Zaccaria "Dal testo alla storia, dalla storia al testo"
Domenico Massaro "La Comunicazione Filosofica 3 - Il pensiero contemporaneo"; "La Comunicazione Filosofica - La grammatica della mente: i ragionamenti deduttivi"
John Allen Paulos "Penso, dunque rido" - Introduzione al primo capitolo: Carroll e Wittgenstein
Maria Cristina Boschini "Alice nel Paese delle Meraviglie di Lewis Carroll: libro per ragazzi o per adulti?" - Articolo tratto dalla rivista online NonSoloCinema
Siti Internet
it.wikipedia.org www.filosofia.unina.it
www2.polito.it/didattica/polymath/
www.adrianopiacentini.it/GodelTeorema
 |
| Appunti su: |
|
| Appunti Economia |  |
| Tesine Ingegneria tecnico |  |