La distribuzione normale o gaussiana

La distribuzione normale o gaussiana

La variabile casuale continua nell'intervallo [a,b],assume qualsiasi  valore dell'intervallo reale( +∞ e -∞)la ciu funzione di densitae indicata con p(x) è definita :

dove m è il valore medio

σ è lo scarto quadratico medio

σ² è la varianza

ottenendo il seguente grafico:

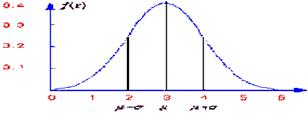
dallo studio di questa funzione otteniamo le seguenti caratteristiche:

• Assume il valore massimo in corrispondenza di m
• Presenta due punti di flesso in corrispondenza di m- σ e m+ σ
• È asintotica rispetto all'asse delle ascisse

Un modo per calcolare la carva di gauss e il calcolo dell'area che sta al disotto della medesima curva attraverso l'integrale definito:

quest'integrale rappresenta la probabilità che la variabile x assuma un valore appartenente [ +∞ ,-∞].

Tale integrale non è pero calcolabile con i normali metodi di integrazione .

Infatti per determinare tale valore sono state compilate delle tabelle per usufruire  delle quali è però necessario operare una translazione del sistema di riferimento, portando l'origine degli assi in m.

Fatto questo, le tabelle forniascono la probabilità che la variabile casuale x cada nell'intervallo.

Detto ciò passiamo quindi all'analisi della curva standardizzata.

Variabile casuale gaussiana standardizzata

Se poniamo                                         m = 0 e σ² = 1

Si ha:

In questo caso le caratteristiche sono:

assume valore massimo in corrispondenza di x = m = 0.

Presenta due punti di massimo in corrispondenza di -1 e +1.

È asintotica rispetto all'asse dell'ascisse.

Detto ciò definiamo i parametri :

m è la media e  σ² è la varianza

la media individua la misurazione della massima densità, infatti spostando la m la curva si sposta sull'asse delle ascise.

La varianza invece caratterizza l'appiattimento più o meno accentuato della curva.