 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2591 | Gradito: |
Leggi anche appunti:Funzione inversaFunzione inversa Una funzione di due Equazione differenziale del secondo ordineEQUAZIONE DIFFERENZIALE DEL SECONDO ORDINE DEFINIZIONE Dicesi equazione La domanda e l'offertaLA DOMANDA E L'OFFERTA La domanda è la quantità di un bene che viene richiesta |
 |
 |
Trasformata di Laplace
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
L[f (t-t)] = e-ts F(s) Traslazione nel tempo
L[ekt f(t)] = F(s - k)
![]()
![]()
![]()
![]()
Teorema del valore
finale ![]()
Teorema del prodotto integrale o di convoluzione L[f(t)*g(t)] = F(s) G(s)
La funzione
caratteristica è ![]() dove t è la costante di tempo.
dove t è la costante di tempo.
Tempo di assestamento: tempo occorrente affinché l'uscita rimanga entro il 5% del valore finale. E' pari a 3t
La funzione di
trasferimento è 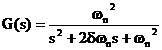 , con d coefficiente di smorzamento e wn pulsazione naturale. Poniamo d = cos j
, con d coefficiente di smorzamento e wn pulsazione naturale. Poniamo d = cos j
Si definisce inoltre
la pulsazione naturale smorzata ![]()
Massima sovraelongazione S: differenza fra il valore massimo raggiunto dall'ascissa e il valore finale . Normalmente si esprime in percentuale del valore finale.
Tempo di ritardo TR: tempo necessario per raggiungere il 50% del valore finale.
Tempo di salita TS: tempo occorrente perché l'uscita passi dal 10% al 90% del valore finale.
Istante di massima sovraelongazione TM o tempo di primo picco TP: istante al quale si presenta la massima sovraelongazione. E' pari a p wd
Massima sovraelongazione percentuale MP ![]()
Tempo di assestamento TS al 5% è ~![]() , al 2% è ~
, al 2% è ~![]()
Tempo di salita TR 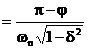
Se d>1 il sistema si dice sovrasmorzato 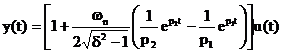
se ![]() il sistema si può
approssimare con un sistema del primo ordine
il sistema si può
approssimare con un sistema del primo ordine ![]()
Se 0<d<1 si ha che 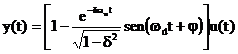
Uno zero a parte reale negativa fa diventare il sistema più veloce.
Sistema a fase minima: non ha né zeri, né poli a parte reale positiva
Perturbiamo un sistema, inizialmente in quiete, con un segnale d'ingresso diverso da zero per un intervallo di tempo di durata limitata.
Comportamento
semplicemente stabile:
risposta limitata ![]()
Comportamento
asintoticamente stabile:
risposta convergente asintoticamente a 0 ![]()
Comportamento instabile: risposta divergente.
Per un sistema non lineare il comportamento può essere diverso al variare del punto di equilibrio e della perturbazione. Un punto di equilibrio si dice globalmente stabile se è stabile per perturbazioni di qualunque entità. Se ciò avviene per un qualunque punto di equilibrio si dice che il sistema è globalmente stabile.
Il comportamento dei sistemi lineari non dipende né dal punto di equilibrio, né dall'entità della perturbazione.
Condizione necessaria e sufficiente per la stabilità semplice è che la funzione di trasferimento non presenti alcun polo a parte reale positiva e che gli eventuali poli a parte reale nulla siano semplici.
Per la stabilità asintotica è necessario e sufficiente che tutti i poli abbiano parte reale negativa.
Quando uno zero e un polo coincidono si possono semplificare.
Quando uno zero e un polo sono vicini tra loro il residuo del polo diminuisce.
|
Per |
Costante di
posizione |
Errore di
posizione |
|
Per |
Costante di
velocità |
Errore di velocità |
|
Per |
Costante di
accelerazione |
Errore di
accelerazione |
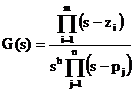
Sistema di tipo zeroh = 0, G(s) non presenta alcun polo nell'origine |
Kp finito T ep finito |
Kv = 0 T ev = |
Ka = 0 T ea= |
Sistema di tipo unoh = 1, G(s) ha un polo semplice nell'origine |
Kp = T ep = 0 |
Kv finito T ev finito |
Ka = 0 T ea= |
Sistema di tipo dueh = 2, G(s) ha un polo doppio nell'origine |
Kp = T ep = 0 |
Kv = T ev = 0 |
Ka finito T ea finito |
Un polo nell'origine migliora la risposta a regime e la sensitività rispetto alle variazioni parametriche e ai disturbi.
Un polo nell'origine si inserisce con un integratore nella catena diretta.
Valori di Kp, Kv, Ka elevati si ottengono inserendo un amplificatore nella catena diretta.
E' un procedimento grafico per la costruzione del tracciato descritto nel piano complesso dalle radici dell'equazione caratteristica al variare di un parametro, normalmente la costante di guadagno d'anello K. Al variare di K da 0 a le radici dell'equazione 1 + G(s) H(s) = 0 descrivono una curva nel piano s, a cui si dà il nome di luogo delle radici.
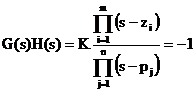 T
T 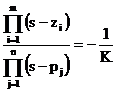
Eq. dei moduli 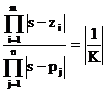 Eq. delle
fasi
Eq. delle
fasi ![]()
Il luogo delle radici ha tanti rami quanti sono i poli della funzione G(s)H(s). I rami, simmetrici rispetto all'asse reale, partono dai poli di G(s)H(s) e terminano negli zeri di G(s)H(s) o in un punto all'infinito.
Per K m rami tendono verso gli zeri ed n - m rami tendono ad
Se K è positiva, un punto dell'asse reale fa parte del luogo delle radici se si lascia alla sua destra un numero totale dispari di zeri e poli. Se la costante K è negativa un punto dell'asse reale fa parte del luogo se si lascia alla sua destra un numero totale pari di zeri e poli.
Se la
costante K è positiva, l'angolo secondo il quale il luogo delle radici lascia
un polo pi è 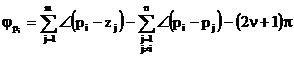 . L'angolo secondo il quale il luogo tende ad uno zero zi
è
. L'angolo secondo il quale il luogo tende ad uno zero zi
è 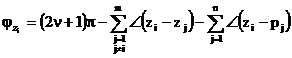 . Se la costante K è negativa si sostituisce 2up a (2u p
. Se la costante K è negativa si sostituisce 2up a (2u p
Una radice multipla di ordine h corrisponde ad un punto comune ad h rami del luogo delle radici, in cui sono soddisfatte le relazioni che esprimono l'annullarsi delle derivate della funzione di guadagno d'anello G(s)H(s) fino alla (h-1)-esima.
In corrispondenza di una radice di ordine h il luogo presenta h rami entranti e h rami uscenti, alternati fra di loro, le cui tangenti dividono lo spazio circostante in settori uguali di p/h radianti.
Gli
asintoti del luogo delle radici formano una stella di raggi con centro nel
punto dell'asse reale di ascissa 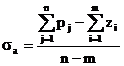 che formano con l'asse reale gli angoli
che formano con l'asse reale gli angoli ![]() se K>0. Se K è
negativa si sostituisce 2up a (2u p
se K>0. Se K è
negativa si sostituisce 2up a (2u p
Le soluzioni di K'(s)=0 sono soluzioni della derivata dell'equazione caratteristica. Si deve verificare che questi punti appartengano al luogo delle radici. Se è difficile risolvere l'equazione K'(s)=0 si possono cercare per tentativi i valori di s per i quali K è massimo o minimo relativo.
ANALISI ARMONICA
Se si applica ad un sistema lineare stazionario asintoticamente stabile il segnale d'ingresso x(t)=Xsen(wt), in condizioni di regime stazionario periodico l'uscita è yr(t)=Y(w)sen(wt+j w
Si definisce funzione di risposta armonica la funzione F(w) di variabile reale a valori complessi avente come modulo il rapporto Y(w)/X e come argomento l'angolo j w
![]()
In un sistema lineare, tempo invariante, asintoticamente stabile, la funzione di risposta armonica F(w) è legata alla funzione di trasferimento G(s) dalla relazione F(w)=G(jw
Essendo la funzione di risposta armonica a valori complessi si impiegano due diversi diagrammi, uno dei quali (detto diagramma delle ampiezze, o dei moduli, o diagramma a) riporta il logaritmo del modulo della risposta armonica in funzione del logaritmo della pulsazione w e l'altro (detto diagramma delle fasi, o degli argomenti, o diagramma b) riporta l'argomento della risposta armonica, sempre in funzione del logaritmo della pulsazione w
Usiamo carta con scala semilogaritmica sia per le ampiezze che per le fasi. La scala delle ampiezze è graduata in decibel. La fase si riporta in gradi. 1db=20LogG(jw
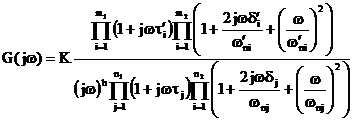
![]()
Possiamo ottenere i diagrammi di G(jw) data in forma fattorizzata come somma di diagrammi elementari corrispondenti ai singoli fattori.
Modulo: retta orizzontale di ordinata ![]() . Fase:
. Fase: ![]()
(jw)-h
(1+jwt
Approssimiamo il diagramma di Bode col diagramma asintotico.
Definiamo w t pulsazione di break.
Modulo
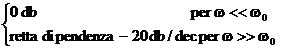
Errore massimo per w w pari a 3db.
Il diagramma reale è al di sotto del diagramma asintotico.
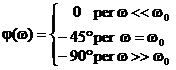 Raccordiamo le 2 rette con la tangente al diagramma nel punto
(w
Raccordiamo le 2 rette con la tangente al diagramma nel punto
(w
I punti di intersezione sono wa w /4.81 e wb w
Se t<0 il diagramma delle ampiezze risulta
immutato con punto di break ![]() , mentre il diagramma delle fasi risulta ribaltato rispetto
all'asse delle ascisse.
, mentre il diagramma delle fasi risulta ribaltato rispetto
all'asse delle ascisse.
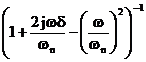
Modulo: asintoti 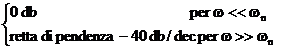
Se d=0 il modulo per w wn è infinito. L'approssimazione con il diagramma asintotico non va bene per piccoli valori di d
Ampiezza di
risonanza MR=![]() è l'ampiezza massima
e si ha in corrispondenza della pulsazione di risonanza
è l'ampiezza massima
e si ha in corrispondenza della pulsazione di risonanza ![]() e con
e con ![]()
Se ![]() la curva interseca
l'asse delle ascisse a destra di wn
la curva interseca
l'asse delle ascisse a destra di wn
Se ![]() la curva interseca
l'asse delle ascisse a sinistra di wn
la curva interseca
l'asse delle ascisse a sinistra di wn
Se ![]() il diagramma
reale è al di sotto del diagramma asintotico
il diagramma
reale è al di sotto del diagramma asintotico
Fase
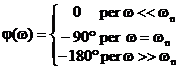 Raccordiamo le 2 rette con la tangente al diagramma reale in
(wn
Raccordiamo le 2 rette con la tangente al diagramma reale in
(wn
Le intersezioni si hanno per wa wn d e wb d wn
Se d=0 la variazione di fase è brusca. La fase è indeterminata.
Se -1<d<0 il sistema è instabile. Il diagramma delle fasi è speculare rispetto all'asse delle ascisse.
Larghezza di banda wb pulsazione alla quale il modulo della risposta armonica è inferiore di 3 db al valore statico G0(0)
Rete ritardatrice: attenua le alte frequenze. Introduce un ritardo di fase w
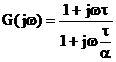 con a<1.
Il massimo ritardo si ha per
con a<1.
Il massimo ritardo si ha per ![]()
Rete anticipatrice: amplifica le alte frequenze. Introduce un anticipo di fase w
![]() con a<1. Il massimo anticipo si ha per
con a<1. Il massimo anticipo si ha per ![]()
Si utilizzano per la rappresentazione della funzione di risposta armonica. Forniscono la curva che rappresenta nel piano di Gauss il variare del numero complesso G(jw) in funzione della pulsazione w. La curva è graduata in valori della pulsazione.
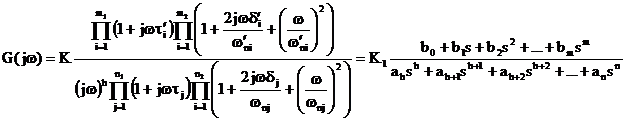
Comportamento per w
Se h=0 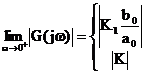
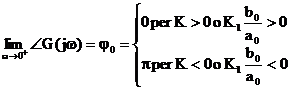
Per studiare il comportamento per piccoli valori di w trascuriamo i termini in w
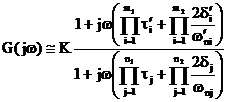
Poniamo ![]() e
e 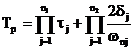
![]()
![]()
Oppure ![]() T
T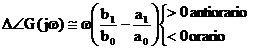
![]()
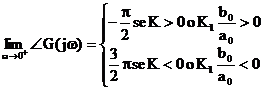
![]() Non è detto che vi
siano asintoti
Non è detto che vi
siano asintoti
Se n = m
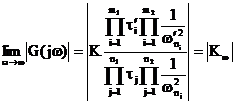
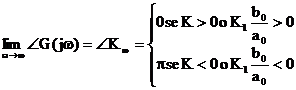
Se n>m
![]()
![]() dove:
dove:
![]() è il numero di poli a
parte reale
è il numero di poli a
parte reale
![]() è il numero di poli a
parte reale > 0
è il numero di poli a
parte reale > 0
![]() è il numero di zeri a
parte reale
è il numero di zeri a
parte reale
![]() è il numero di zeri a
parte reale > 0
è il numero di zeri a
parte reale > 0
Consente di stabilire se un sistema, del quale si conosca la risposta armonica ad anello aperto sia stabile o meno una volta chiuso in retroazione. Costituisce anche un'utile guida per valutare l'efficacia di possibili interventi che, attraverso opportune modifiche della funzione di risposta armonica ad anello aperto, migliorino il comportamento dinamico del sistema in retroazione.
N = Z - P
Dove N è il numero di rotazioni in senso orario del diagramma di Nyquist intorno al punto -1 + j0, Z è il numero degli zeri a parte reale positiva dell'equazione caratteristica e P è il numero di poli a parte reale positiva della funzione di trasferimento in anello aperto.
SINTESI
La rete ritardatrice riduce il guadagno alle alte frequenze senza influire sulla costante di guadagno. L'inconveniente principale è la riduzione del guadagno alle alte frequenze. Questo si traduce in una risposta transitoria meno pronta e in una neutralizzazione dei disturbi ad alta frequenza meno efficace.
Scegliamo come
frequenza di cross-over di guadagno del sistema compensato ![]() la frequenza in
corrispondenza della quale sul diagramma delle fasi si legga il margine di fase
desiderato.
la frequenza in
corrispondenza della quale sul diagramma delle fasi si legga il margine di fase
desiderato.
Imponiamo quindi che
20 Log a = - 20 Log G(j![]() )
)
Da questa relazione determiniamo a
Dalla relazione ![]() ricaviamo t. Imponiamo una distanza tale da impedire che
il ritardo di fase introdotto dalla rete ritardatrice abbia influenza in
corrispondenza di
ricaviamo t. Imponiamo una distanza tale da impedire che
il ritardo di fase introdotto dalla rete ritardatrice abbia influenza in
corrispondenza di ![]() .
.
N.B. Le reti ritardatrici non si possono utilizzare per compensare sistemi di tipo 2, perché questi sistemi hanno una fase sempre inferiore a -180°.
Determino K in base alla specifica sull'errore a regime.
Disegno il diagramma di Bode.
Verifico se il MF soddisfa la specifica.
Se la
specifica su MF non è verificata assumo ![]() =MF + e con e
=MF + e con e
Determino
![]()
Determino
a dalla relazione
20 Log a = - 20 Log G(j![]() )
)
Determino
t dalla relazione ![]()
Se la specifica su MF è verificata mi fermo, altrimenti torno al punto 4.
Vogliamo fare in modo che la rete
anticipatrice introduca il massimo anticipo di fase jm in corrispondenza della frequenza di
cross-over di guadagno del sistema compensato ![]() .
.
Perciò imponiamo che sia ![]() = wm =
= wm = ![]() . L'anticipo di fase jm dev'essere tale da portare il margine di fase ad un valore che
soddisfi la specifica.
. L'anticipo di fase jm dev'essere tale da portare il margine di fase ad un valore che
soddisfi la specifica.
Si imporrà quindi jm = MF desiderato - MF sistema + e con 5°<e<20°
e è un coefficiente di sicurezza che si
introduce a causa dello spostamento verso destra di ![]() dovuto
all'amplificazione. e è tanto maggiore quanto maggiore è la
velocità con cui la fase diminuisce all'aumentare di w
dovuto
all'amplificazione. e è tanto maggiore quanto maggiore è la
velocità con cui la fase diminuisce all'aumentare di w
Possiamo quindi determinare a dalla relazione ![]() .
.
La rete anticipatrice aumenta il guadagno alle alte frequenze e quindi la larghezza di banda. Questo significa che si ottiene una risposta più pronta.
Se jm > 60° si introducono 2 reti anticipatrici.
Determino K in base alla specifica sull'errore a regime.
Disegno il diagramma di Bode.
Verifico se il MF soddisfa la specifica.
Se la specifica su MF non è verificata pongo jm = MF desiderato - MF sistema + e con 5°<e<20° .
Determino
a dalla relazione ![]() .
.
Determino
![]() dalla relazione 10 Log
a = 20 Log G(j
dalla relazione 10 Log
a = 20 Log G(j![]() )
)
Determino
t dalla relazione ![]() = wm =
= wm = ![]() .
.
Se la specifica su MF è verificata mi fermo, altrimenti torno al punto 4.
 |
| Appunti su: appunti controlli automatici, |
|
| Appunti Statistica |  |
| Tesine Contabilita |  |
| Lezioni Geografia |  |