 |
|
| Appunti universita |
|
 |
|
| Appunti universita |
|
| Visite: 3190 | Gradito: |
Leggi anche appunti:Scienza delle finanzeSCIENZA DELLE FINANZE 1. E-commerce L’area Scienze delle finanzeSCIENZE DELLE FINANZE Evoluzione storica dell’ordinamento L’assegno circolareL’ASSEGNO CIRCOLARE L'assegno circolare è un titolo di credito all'ordine |
 |
 |
COMBINAZIONE OTTIMA DEI FATTORI DI PRODUZIONE- LA FUNZIONE DI COBB-DUGLAS
Problema tipico di un’impresa è trovare la combinazione ottima dei fattori di produzione.
Fra i fattori di produzione si considerano in modo specifico il capitale impiegato K e la quantità di lavoro utilizzata L. La funzione di produzione è data dal massimo profitto che si può ottenere dalle diverse combinazioni di capitale e lavoro: Q=f(K,L)
Come abbiamo visto, in Cina si può contare su un basso costo del lavoro e questo inciderà in modo positivo sulla funzione, permettendo alle imprese di sostenere minori costi per questo fattore di produzione. Ma vediamo come si può organizzare la produzione all’interno delle imprese al fine di permettere una migliore organizzazione ed un minore dispendio di risorse.
Di uso frequente è la funzione di Cobb-Douglas impiegata per descrivere tipi di produzioni che non richiedono l’impiego dei fattori produttivi in proporzioni fisse.
Spazio
Paul Howard Douglas, uno dei due inventori della funzione
 Nato il 26 marzo 1892, nella piccola
città di Salem, Massachusetts. Si laureò al Bowdoin College nel 1913, quindi si
spostò alla Columbia University, dove guadagnò un master in economia.
Nato il 26 marzo 1892, nella piccola
città di Salem, Massachusetts. Si laureò al Bowdoin College nel 1913, quindi si
spostò alla Columbia University, dove guadagnò un master in economia.
Nel 1915 sposò Dorothy Wolff e nei successivi sei anni studiò all’università di Harvard, insegnò nell’univerità dell’Illinois, nell’Oregon's Reed College, e nell’università di Washington. Durante questi anni si convertì, inoltre, all’episcopalismo e si unì alla società degli amici religiosi.
Douglas amava il suo lavoro, ma la moglie era incapace di trovare una occupazione all’università a causa delle regole sull’anti-nepotismo. Quando ottenne un lavoro allo Smith College, convinse suo marito a trasferirsi con lei e ad insegnare all’università del Massachusetts Amherst. Douglas presto decise che la situazione era insopportabile, così nel 1930 la coppia divorziò: Dorothy prese i loro quattro figli in custodia e Douglas tornò a Chicago. Negli anni seguenti però Douglas incontrò e sposò Emily Taft.
Verso la fine degli anni venti, Douglas iniziò ad interessarsi alla carriera politica. Servì da consigliere economico a due governatori, lanciò una campagna contro le manipolazioni del
mercato azionario, aiutò nel regolare progetti di legge concernenti le pensioni di vecchiaia e la
disoccupazione. Nei primi anni trenta, divenne vice presidente della lega di azione politica indipendente, membro del comitato nazionale del partito coltivatore-lavoro e tesoriere della federazione politica del commonwealth americano.
Nel 1932 scrisse un libro, intitolato The Coming of a New Party( la venuta di un nuovo partito) nel quale esprimeva le proprie opinioni politiche, ossia che il partito democratico era troppo corrotto ed il partito repubblicano era troppo reazionario. Divenne sindaco di Chicago nel 1935, ma le sue riforme nel campo dell’educazione e dei trasporti non furono apprezzate.
Nel 1942 si dimette quindi dalla propria carica e si unisce al corpo dei Marines.
In seguito Douglas si unisce al partito democratico e si candida per il senato, aspirando a divenire governatore dell’Illinois; la partecipazione a varie e vittoriose guerre resero Douglas un eroe conosciuto e ciò, oltre al fatto che molti scandali avevano colpito in quel periodo gli
avversari, permise a Douglas di realizzare le sue speranze. La sua carica va dal 1949 al 1967, anno in cui perse le elezioni per vari motivi: infelicità all’interno del partito democratico per la sua volontà di sostenere la guerra in Vietnam ma anche per la sua età (era ormai settantacinquenne).
Muore il 24 settembre 1976.
Tornando alla funzione…
Supponendo che l’impresa impieghi come input il lavoro (L) e il capitale (K) la funzione di produzione è rappresentata dalla seguente espressione:
Q = AKa Lb
In cui Q indica appunto la quantità prodotta, 0<a<1 e 0<b<1
A è una costante moltiplicativa che può essere considerata un indicatore del grado di efficienza nell'utilizzo di tutti i fattori di produzione. È dunque un parametro di efficienza che indica il livello della tecnologia. a e b rappresentano invece dei coefficienti che consentono di analizzare alcune caratteristiche della tecnologia impiegata, quali i rendimenti di scala e l’elasticità di sostituzione.
Per comprendere le caratteristiche della funzione di produzione Cobb-Douglas, supponiamo che:
A = 1; K = 4; L = 2 e che a = 1/2 e b =1/2. (a+b=1)
Allora si avrà:
Y = 1 × 41/2 × 91/2 = 6
Quindi, se si impiegano 9 unità di lavoro e 4 di capitale, la tecnologia consente di ottenere 6 unità di output. Se moltiplichiamo ciascun fattore per un certo numero, poniamo 2, l’output prodotto raddoppia passando a 12. Con a + b =1, dunque, si hanno rendimenti di scala costanti.
Infatti: f(2K,2L) = A(2K)a (2L)b = A 2a+b Ka Lb = 2a+b (AKa Lb) = 2Q
Se a + b >1, la tecnologia presenta rendimenti di scala crescenti: moltiplicando tutti i fattori per una costante l , l’output aumenta più che proporzionalmente. f(2K,2L) = 2a+b Q>2Q
L’opposto accade nel caso in cui a + b < 1. f(2K,2L) = 2a+b Q<2Q
Due sono i problemi che si possono presentare:
Minimizzare il costo totale dei fattori di produzione (input) per produrre una quantità prefissata di bene (output).
Massimizzare la produzione ad un livello di costi prefissato.
Problema 1 – Minimo costo con vincolo della produzione.
Dati i prezzi degli input e gli output, bisogna associarvi il costo minimo che è necessario sostenere per la loro produzione.
Bisogna quindi minimizzare la funzione del costo.
C=rK+wL
Dove r è il costo unitario del capitale e w è il costo unitario del lavoro.
Il vincolo è dato dalla relazione Q0 =f(K,L)
Il problema si può risolvere mediante il metodo dei moltiplicatori di Lagrange o mediante le linee di livello.
Metodo dei moltiplicatori di Lagrange:
La funzione lagrangiana è: Z=rK+wL+l(Q0 - f(K,L))
Procedendo con il metodo dei moltiplicatori di Lagrange, si calcolano le derivate parziali prime rispetto a K, L, l e dopo averle annullate le si pongono a sistema.
Linee di livello:
Queste linee di livello vengono chiamate isocosti perchè ognuna di esse rappresenta tutte le combinazioni di lavoro e capitale (L,K) che lasciano invariato il costo.
Si rappresentano su uno stesso sistema cartesiano gli isocosti e la curva del vincolo. Si procede quindi alla determinazione della retta di isocosto tangente alla curva della produzione.
Problema 2 – Massima produzione con vincolo del costo.
Il problema consiste nel determinare la distribuzione ottima dei due fattori di produzione (K.L) in modo da massimizzare la quantità prodotta, essendo prefissato il costo.
Bisogna quindi massimizzare la funzione
Q =f(K,L)
Con il vincolo C0 =rK+wL
Come per il problema precedente, anche questo si può risolvere mediante il metodo dei moltiplicatori di Lagrange o mediante le linee di livello.
La funzione lagrangiana sarà questa volta: Z= f(K,L)+l(C0 -rK+wL)
Le linee di livello sono chiamate isoquanti perché ognuna di esse rappresenta tutte le combinazioni di lavoro e capitale (L,K) che lasciano invariata la quantità di prodotto.
Dimostrazione pratica
Per la produzione di un bene un’impresa sostiene un costo di produzione espresso dalla funzione: C(L,K)=12L+8K dove L=unità di lavoro e K=unità di capitale
Sapendo che la funzione di produzione è data da:
Q=10K0,4 L0,6
E che l’impresa deve produrre 400 unità del bene, determinare come deve combinare i fattori produttivi in modo che il costo sia minimo.
Risoluzione:
Questo problema è del tipo
Metodo dei moltiplicatori di Lagrange:
Funzione costo: C=12L+8K
Vincolo di produzione: Q=10K0,4 L0,6
Dove Q=400 e pertanto il vincolo sarà: 10K0,4 L0,6=400
La funzione lagrangiana è: Z=8K+12L+l(400-10 K0,4 L0,6)
Calcolo le derivate parziali prime rispetto a K, L, l
Z/ K= 8-0,4*10 l K-0,6 L0,6
Z/ L=12-0,6*10 l K0,4 L-0,4
Z/ l= 400-10 K0,4 L0,6
Le annullo e le pongo a sistema:
![]() l K-0,6 L0,6=0
l K-0,6 L0,6=0
l K0,4 L-0,4=0
10 K0,4 L0,6=400
Risolvo quindi il sistema al fine di trovare il valore di K, L e l
![]()
![]()
![]()
l K-0,6 L0,6=2 l K-0,6 L0,6=2 l K-0,6 L0,6=2
l K0,4 L-0,4=2 l K0,4 L-0,4=2 l K0,4 L-0,4=2
K0,4 L0,6=40 K 2/5=40 L -3/5 K=405/2 L-3/2 (*)
![]()
![]()
l (405/2 L-3/2)-0,6 L0,6=2 l 40-3/2 L9/10 L6/10=2
l (405/2 L-3/2)0,4 L-0,4=2 l 40 L-3/5 L-2/5=2
(*)
![]()
![]()
![]()
l 40-3/2 L3/2=2 l 40-3/2 L3/2=2 (1/20) L 40-3/2 L3/2=2
l 40 L-1=2 l =(1/20) L l =(1/20) L
(*) (*)
![]()
![]()
![]()
![]()
L5/2=403/2 *20*2 L5/2=405/2 L=40 L=40
l =(1/20) L l =(1/20) L l l
(*) (*) K=405/2 40-3/2 K=40
Vado ora a sostituire i valori ottenuti, all’interno della funzione Z per trovare il valore del minimo costo:
![]() Z=8K+12L+l(400-10 K0,4 L0,6) Z=8*40+12*40+l
Z=8K+12L+l(400-10 K0,4 L0,6) Z=8*40+12*40+l
![]() Z=320+480+2*0 Z=800
Z=320+480+2*0 Z=800
Quindi: il costo minimo si ottiene impiegando 40unità di capitale e 40unità di lavoro ed è di €800.
Mediante le linee di livello:
Risolviamo ora lo stesso problema con il metodo delle linee di livello e verifichiamo il risultato.
Funzione costo: C=12L+8K
Vincolo di produzione: Q=10K0,4 L0,6
Dove Q=400 e pertanto il vincolo sarà: 10K0,4 L0,6=400
Gli isocosti sono quindi segmenti di rette.
Assegno al costo totale C i valori 400, 800, 1200 e 1600 per poter rappresentare sul piano cartesiano degli isocosti e la curva del vincolo.
Le rette degli isocosti (12L+8K=?) hanno coefficiente angolare -3/2.
Il grafico risulta come segue:
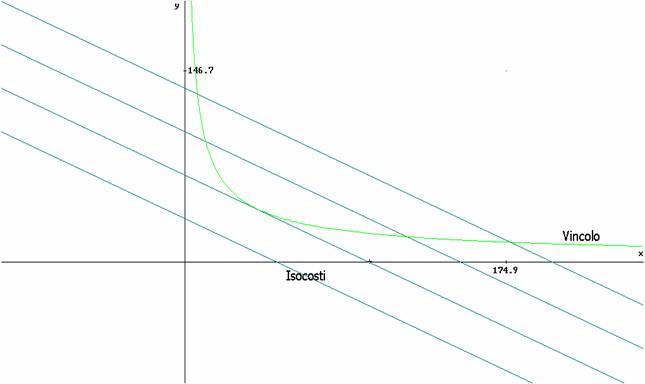
Dato che il coefficiente angolare è uguale alla derivata nel punto di tangenza, esplicito la variabile K dal vincolo per poter poi calcolare la derivata rispetto ad L, quindi:
![]() 10K0,4 L0,6=400 10K4/10
L6/10=400
10K0,4 L0,6=400 10K4/10
L6/10=400
10K2/5 =400 L-3/5
K=405/2 L-3/2
K/ L = (-3/2)*405/2 L5/2
Se poniamo quindi la derivata uguale al coefficiente angolare possiamo ottenere il valore di L:
![]() (-3/2)*405/2
L5/2=-3/2 L5/2=402/5
(-3/2)*405/2
L5/2=-3/2 L5/2=402/5
L=40 c.v.d.
Se sostituiamo il valore ottenuto di L nel vincolo, ricaviamo K:
![]() 10K0,4 L0,6=400 10K4/10 406/10=400
10K0,4 L0,6=400 10K4/10 406/10=400
10K2/5 =400*40-3/5
K=405/2 *40-3/2
K=40 c.v.d.
Sostituiamo L e K nella funzione costo per vedere qual è il costo minimo:
![]() C=12L+8K C=12*40+8*40
C=12L+8K C=12*40+8*40
C=800 c.v.d.
I risultati ottenuti coincidono.
 |
| Appunti su: combiazione ottima dei fattori produttivi con langrage, calcolo combinazione ottima lavoro e capitale, combinazione ottima di due fattori, trovare la combinazione ottima di fattori, |
|
| Appunti costruzione |  |
| Tesine Agricoltura agraria |  |
| Lezioni Economia |  |