 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 5406 | Gradito: |
Leggi anche appunti:Ricerca operativa. Problemi di decisioneRicerca operativa. Problemi di decisione Scopi e metodi della ricerca operativa. La Criteri di convergenzaCriteri di convergenza Per stabilire se una serie sia convergente Insiemi numerici e progressioniINSIEMI NUMERICI E PROGRESSIONI La parola insieme è sinonimo di aggregato, |
 |
 |
RUSSELL E PEANO: LA FILOSOFIA DELLA MATEMATICA
"La filosofia è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi a gli occhi (io dico l'universo), ma non si può intendere se prima non s'impara a intender la lingua, e conoscer i caratteri, ne' quali è scritto. Egli è scritto in lingua matematica, e i caratteri son triangoli, cerchi, ed altre figure geometriche, senza i quali mezi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro laberinto."
Galileo Galilei
 GIUSEPPE PEANO
GIUSEPPE PEANO
Giuseppe Peano (Spinetta di Cuneo, 27 agosto 1858 - Torino, 20 aprile 1932) è stato un matematico e glottoteta italiano. Insegnò calcolo infinitesimale a Torino a partire dal 1890. Precisò la definizione del limite superiore, fornì il primo esempio di una curva che riempie una superficie (Curva di Peano) (uno dei primi esempi di frattale) mettendo così in evidenza come la definizione di curva allora vigente non fosse conforme a quanto intuitivamente si intende per curva. Fu uno dei padri del calcolo vettoriale insieme a Tullio Levi-Civita. Dimostrò importanti proprietà delle equazioni differenziali ordinarie, e ideò un metodo di integrazione per successive approssimazioni. Era affascinato dall'ideale leibniziano della lingua universale, e adottò il latino sine flexione, con cui teneva le sue lezioni. Nella logica diede una versione assiomatizzata della matematica, i famosi assiomi di Peano, i quali vennero ripresi da Russell e Whitehead nei loro Principia Matematica per sviluppare la teoria delle classi. Vittima del suo stesso eccentricismo, che lo portava ad insegnare logica in un corso di calcolo infinitesimale e a non fare mai esami, venne più volte allontanato dall'insegnamento, a dispetto della sua fama internazionale. Ricordi e non solo della vita familiare del grande matematico, sono raccontati con grazia e ammirazione nel romanzo biografico Giovinezza Inventata della pronipote, scrittrice e poetessa Lalla Romano. Morì nella sua casa di campagna vicino a Torino per un attacco di cuore che lo colse nella notte.
Per presentare la figura di Peano, propongo il giudizio dato sul personaggio da Bertrand Russell:
"Il congresso segnò una svolta importante nella mia vita intellettuale perché fu in quell'occasione che incontrai Peano. Lo conoscevo già di nome e avevo letto alcune delle sue opere, ma non mi ero preso la briga di assimilare i suoi simboli. Durante le discussioni del congresso mi resi conto che era sempre più preciso di tutti gli altri e che in tutte le discussioni risultava invariabilmente il più brillante. Con il passare dei giorni mi convinsi che questo dipendeva dalla sua logica matematica e pertanto mi feci dare da lui tutte le sue opere e non appena il congresso si chiuse mi ritirai a Fernhurst per studiare in tutta tranquillità tutto ciò che lui e i suoi discepoli avevano scritto. Mi resi conto che il suo metodo di notazioni forniva quello strumento di analisi logica che per anni avevo cercato, e che studiando l'opera sua mi stavo impadronendo di una nuova e potente tecnica per il lavoro che da molto tempo desideravo fare'.
A prima vista l'attività scientifica di Peano sembra spaziare nei campi più disparati, dall'analisi alla geometria, dall'aritmetica alla logica. In realtà, dietro all'apparente eclettismo della sua opera si nasconde un unitario interesse per i fondamenti della matematica, dal quale egli derivò lo stimolo per l'analisi delle nozioni più comuni delle varie branche della matematica. Volendo collocare Peano nell'ambito della ricerca sui fondamenti, lo si deve considerare contrapposto alla contemporanea tradizione di Frege e Russell, e allineato invece a quella di Hilbert. E' uno degli iniziatori del simbolismo moderno, difatti si fa promotore di una notazione simbolica che permette di ridurre gli enunciati matematici alle proposizioni della logica senza ricorrere al linguaggio naturale. Tale notazione, semplice ed efficace, fu talmente apprezzata dal grande Bertrand Russell, (che di Peano fu grande ammiratore), da fargli riscrivere per intero il suo più grande trattato (I principi della matematica) adottando la notazione formale introdotta dal matematico. Egli riteneva, infatti, che i concetti della matematica non dovessero essere ridotti a più fondamentali nozioni logiche, bensì che di ogni disciplina, logica compresa, si dovessero autonomamente isolare i concetti primitivi, descrivendone poi assiomaticamente le proprietà fondamentali.
"..in ogni scienza, dopo aver analizzato le idee, esprimendo le più complicate per mezzo della più semplici, se ne trovano un certo numero che non si possono più definire. Sono le idee primitive della scienza; bisogna acquisirle per esperienza o per induzione; è impossibile spiegarle per deduzione.."
La sostanza dell'approccio assiomatico di Peano si può facilmente enunciare:
assiomi sono arbitrari,
nozioni primitive sono definite implicitamente dagli assiomi,
definizioni sono convenzionali.
" .le definizioni sono utili, ma non necessarie, poiché al posto del definito si può sempre sostituire il definiente, e perciò eliminare da tutta la teoria il definito...se eliminiamo il simbolo definito, la nuova esposizione non è più lunga e più complicata della precedente, ciò significa che quella definizione era poco utile.."
Il tutto in netta contrapposizione all'approccio euclideo, che richiedeva l'evidenza e la verità degli assiomi, e l'oggettività delle nozioni primitive e delle definizioni.
La storia, comunque, gli ha poi dato ragione: i matematici si sono, infatti, disinteressati della riduzione unitaria della matematica alla logica o alla teoria degli insiemi, considerando queste ultime come puri strumenti, cioè mezzi e non fini. L'organizzazione assiomatica per discipline separate è invece divenuta un riferimento essenziale e uno strumento obbligato della matematica moderna.
Ma gli interessi di Peano non si riducevano semplicemente alla matematica.
Inventò infatti il latino sine flexione, una versione semplificata del latino classico (anticipata in parte da Leibniz), in cui tutte le difficoltà delle terminazioni (declinazioni) sono soppresse; tale lingua doveva servire, nelle intenzioni dell'autore, alla comunicazione scientifica internazionale; il progetto attirò inizialmente una certa attenzione, soprattutto grazie alla reputazione dell'autore, ma non conobbe mai un grande successo, e fu poi molto criticato.
Nonostante ciò Peano pubblicò numerosi testi in questa lingua e la utilizzò per tenere le sue lezioni. Ecco un esempio di scrittura in tale lingua:
'Latino es lingua internationale in occidente de Europa ab tempore de imperio romano, per toto medio aevo, et in scientia usque ultimo seculo. Seculo vigesimo es primo que non habe lingua commune. Hodie quasi omne auctore scribe in proprio lingua nationale, id es in plure lingua neo-latino, in plure germanico, in plure slavo, in nipponico et alio. Tale multitudine de linguas in labores de interesse commune ad toto humanitate constitute magno obstaculo ad progressu.'
Esempio più eclatante di tale lingua è l'opera del 1889 Arithmetices Principia nova methodo exposita , tutta in latino, nella quale realizzava la prima sistemazione assiomatica dell'intera matematica (o quasi), ottenendo l'eclatante risultato di ridurre tutta l'analisi e l'aritmetica al sistema dei numeri naturali, e di ridurre a sua volta quest'ultimo a tre idee primitive e cinque assiomi:
Esiste un numero naturale, 0 (o 1)
Ogni numero naturale ha un numero naturale successore
Numeri diversi hanno successori diversi
0 (o 1) non è il successore di alcun numero naturale
Ogni insieme di numeri naturali che contenga lo zero (o l'uno) e il successore di ogni proprio elemento coincide con l'intero insieme dei numeri naturali (assioma dell'induzione)
Nel 1890 pubblica Sur une courbe qui
remplit toute une aire plane, dove per la prima volta al mondo si parla di
una curva che copre tutti i punti di un quadrato:
La curva di Peano ha scosso il mondo matematico tanto
che Hilbert definì le curve costruite in modo analogo 'Curve
Mostruose'.
Lo sconcerto è comprensibile, perché curve come quella di Peano mappano, in modo ricorsivo, con uniforme continuità segmenti in aree del piano.
Il procedimento ricorsivo è definito partendo da un elemento di base come quello definito in
figura 1
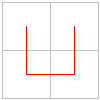
Fig. 1 Elemento Base
Nel passo successivo, la figura viene costruita replicando per quattro volte l'elemento base riducendone le dimensioni a un quarto delle originali, mantenendo inalterato l'orientamento delle due copie inferiori e ruotando di 90 gradi a sinistra e a destra le due copie superiori. Inoltre, effettuano le connessioni come da figura 2 (le connessioni sono evidenziate in nero)
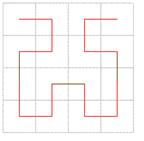
Fig. 2 Seconda Iterazione
(Il lato del quadrato ha dimensione costante pari ad 1, le figure hanno dimensioni crescenti solo per chiarezza). La figura 3 illustra il terzo passo dell'iterazione, che consiste nel replicare quattro volte la figura del passo precedente, ridotta di un fattore 4, applicando le operazioni di rotazione e di connessione definite.

Fig. 3 Terza Iterazione
Iterando all'infinito, si ottiene una 'curva limite' che copre interamente l'area a disposizione.
Si osservi che ogni iterazione suddivide il quadrato originario in quadrati di dimensioni più piccole, contenenti repliche in scala della curva del passo base. Questa proprietà è tipica delle curve 'frattali', di cui possiamo trovare ottimi esempi in natura (i profili delle coste, la struttura dei fiocchi di neve, la geometria del fogliame .).
In conclusione possiamo certamente desumere che la
figura del grande Peano non va certamente confinata nell'ambito puramente
geometrico-matematico, anzi il suo impegno è tangibile nella maggior parte
degli ambiti culturali. Egli era molto attento alle problematiche sociali del suo tempo.
Estremamente affabile e disponibile con i suoi allievi ed impegnato nelle
organizzazioni per l'educazione primaria e secondaria, comprende l'importanza
di far amare la matematica: nel 1925, ad esempio, pubblica il libro Giochi
di aritmetica e problemi interessanti, con lo scopo di rendere
dilettevole e meno noioso lo studio dell'aritmetica per i bambini che hanno
paura della matematica.
Muore per un attacco di cuore mentre ancora è pieno di vita e di interessi.
BERTRAND RUSSELL

Bertrand Russell (1872-1970) nacque in Inghilterra, a Ravenscroft, da nobile famiglia; rimase presto orfano e fu educato dal nonno, lord John Russell.
Nel periodo 1890-94 effettuò i suoi studi a Cambridge dove si interessò soprattutto di matematica e di filosofia e nel 1895 divenne membro del Trinity College.
Gli interessi per la matematica e per la
logica lo portarono a studiare Leibniz, in cui trovava espressa la tesi che i
princìpi della matematica sono deducibili da princìpi logici tramite mezzi
meramente logici: il risultato fu il volume Esposizione critica della
filosofia di Leibniz del 1900. Ad avviso di Russell, il 1900 fu un anno
decisivo della sua vita, perchè prendendo parte al Congresso internazionale di
filosofia, tenutosi a Parigi, incontrò Giuseppe Peano e fu colpito dalla
precisione da questi dimostrata nelle discussione, grazie all'impiego di un
rigoroso simbolismo logico. Il risultato più apprezzabile di questa prima fase
della riflessione di Russell é costituito da I princìpi della matematica
, pubblicati nel
Nel 1912 Russell pubblicò una fortunata esposizione divulgativa del suo pensiero, I problemi della filosofia , e nel 1914 fu inviato a tenere una serie di lezioni ad Harvard, a Boston e ad Oxford, dalle quali ebbe origine il volume La nostra conoscenza del mondo esterno , del 1914. Durante la guerra, per via della sua attività pubblica a favore del movimento pacifista, Russell fu allontanato dall'insegnamento a Cambridge e condannato a sei mesi di reclusione in carcere, durante i quali compose l' Introduzione alla filosofia matematica . Da allora la sua attività filosofica fu sempre intrecciata a battaglie politiche e sociali; nel 1920 fece un viaggio nell'Unione Sovietica, di cui condannò il totalitarismo nel volume Teoria e pratica del bolscevismo (1920). Nel 1920-1921 insegnò a Pechino e nel 1927 aprì con la seconda moglie una scuola sperimentale, dove era applicata una pedagogia non autoritaria. Tutto questo, unitamente ad una serie di scritti popolari, come L'educazione dei nostri figli (1926) , Matrimonio e morale (1929) , La conquista della felicità (1930) , Religione e scienza (1935), nei quali abbracciava posizioni spregiudicate su questioni religiose ed etiche, anche nel campo dell'etica sessuale, suscitò critiche dei benpensanti.
Nel frattempo, Russell proseguiva i suoi studi filosofici, influenzato anche dalle teorie di Wittgenstein, che era stato suo allievo a Cambridge prima della guerra. I vari saggi, tra i quali anche la prefazione da lui scritta alla traduzione inglese del Tractatus logico-philosophicus (1922), espose le linee di una filosofia che egli definì 'atomismo logico' e nel 1927 pubblicò il saggio Analisi della materia . Soprattutto a partire dal 1938, Russell tornò ad intensificare le sue ricerche filosofiche, tenendo lezioni a Oxford, Chicago e Los Angeles. Nel 1940 gli fu offerto un incarico di insegnamento a New York, ma accusato di immoralità per le sue idee anticonformiste ne fu poi allontanato. Nel 1944, Russell rientrò in Inghilterra e ricevette un incarico di insegnamento a Cambridge, che egli tenne fino al 1950: frutto di tale insegnamento fu la sua vasta ed ultima opera filosofica, La conoscenza umana , del 1948. Nel 1950 ricevette il premio Nobel per la letteratura e successivamente prese posizione contro il maccartismo, propugnò il pacifismo e propose il disarmo unilaterale senza condizioni. Nel 1961 capeggiò un sit-in di protesta di fronte al Ministero britannico della Difesa e fu condannato a due mesi di carcere, ridotti ad una settimana a causa delle sue cagionevoli condizioni di salute. Nel 1967, poco prima che sopraggiungesse la morte, iniziò la pubblicazione delle sue memorie, intitolate Autobiografia ; nel 1970 lo colse la morte.
Oltre a una lunga e varia carriera, Russell fece importanti rivelazioni sui fondamenti della matematica e sullo sviluppo della logica formale contemporanea, come anche sulla filosofia analitica.
I suoi contributi riguardo alle matematiche includono la scoperta del paradosso di Russell, la sua difesa del logicismo (la visione che la matematica sia riducibile a una logica formale), la sua introduzione della teoria dei generi, e il suo perfezionamento e divulgazione del calcolo dei predicati di primo ordine.
Fondamentale nell'opera e nel pensiero di Russell è certamente Peano grazie al quale si avvia allo studio delle relazioni tra matematica e logica.
Peano aveva dimostrato che é possibile costruire l'intera teoria dei numeri naturali partendo da tre concetti fondamentali (zero, numero e successore immediato) e da 5 assiomi; per Russell questi tre concetti di Peano sono riducibili alle nozioni logiche di classe e di relazione. Questo vuol dire che la conoscenza matematica può essere pienamente giustificata mostrandone la derivabilità da queste nozioni meramente logiche. Egli avrebbe assolto a questo compito per mezzo della costruzione, tramite i simboli della logica, di un edificio puramente formale nei Principia mathematica , composti insieme a Whitehead: qui i teoremi della matematica pura sono dedotti a partire dalla definizione di zero, numero e successore, usando regole di derivazione delle proposizioni. Questa derivazione é attuata grazie all'ausilio di 4 operatori o costanti logiche: 'non' (negazione), 'e' (congiunzione), 'o' (disgiunzione) e 'se, allora' (implicazione).
Russell é convinto che la matematica pura é la classe di tutte le proposizioni che hanno la forma dell'implicazione e che é compito della logica analizzare questa relazione.
Ma per dimostrare che la matematica si fonda sulla logica, si deve anche dimostrare che i numeri naturali e, quindi, tutte le nozioni fondamentali dell'aritmetica, sono definibili in termini di classe . I numeri non coincidono con le classi di oggetti che sono contati, ma sono quel che tutte queste collezioni di oggetti hanno in comune. Russell definisce pertanto il numero cardinale come ' la classe di tutte le classi simili ad essa ' , cioè di tutte le classi i cui membri possono essere correlati uno ad uno. In tal modo ogni discorso aritmetico su numeri é formulabile nei termini di un discorso meramente logico riguardante le classi e le loro relazioni. Ben presto tuttavia Russell prese atto che il concetto di classe, o di insieme, può dar luogo ad antinomie o paradossi . In particolare, il pensatore inglese individuò, già al termine della stesura dei Principi di matematica , una contraddizione relativa alla nozione di 'classe di classi' , la quale é essenziale per definire i numeri naturali. Egli distinse tra classi che non sono membri di se stesse, cioè non contengono se stesso come elemento e classi che invece lo sono.
A questo punto si pone l'interrogativo: la classe di tutte le classi, che non sono membri di se stesse, é membro di se stessa? Se si dice 'sì' , essa é una classe che é membro di se stessa, ma allora contiene se stessa come elemento e, quindi, non é più la classe di tutte le classi che non contengono se stesse come elemento. Se si dice 'no', essa é una classe che non é membro di se stessa, ma allora appartiene alla classe delle classi che non contengono se stesse come membro e, quindi, contiene se stessa come elemento. Quale che sia la risposta data, ne consegue sempre e comunque l'opposto rispetto ad essa: questo vuol dire che la nozione di classe di tutte le classi che non contengono se stesse come elemento genera contraddizioni. Questa antinomia faceva vacillare il programma logistico: quale é l'utilità nel definire i numeri in termini di classi, se la nozione di classe genera contraddizioni?
Per risolvere questo problema, Russell elaborò la cosiddetta teoria dei tipi : a suo parere, i paradossi nascono da un circolo vizioso, consistente nel ' supporre che una collezione di oggetti possa contenere membri definibili solo tramite la collezione presa come un tutto ' . Per evitare questo circolo vizioso, che consiste nell' autoriferimento di una totalità o di una classe a se stessa, bisogna evitare che tale totalità sia predicata di se stessa e far sì che qualunque asserzione su di essa cada fuori dalla totalità stessa. Per Russell a questo si può provvedere distinguendo tra vari livelli o tipi di oggetti e predicati: di tipo 1 sono gli individui (ad es. Socrate), di tipo 2 sono le proprietà o le classi di individui (ad es, l'umanità), di tipo 3 sono le proprietà o le classi di proprietà e così via. Il paradosso delle classi sorge dal presumere che tutte le classi siano di un tipo solo, mentre é fondamentale che le proprietà di un livello o tipo superiore siano applicate, vale a dire predicate, solamente ad oggetti di tipo inferiore. Questo vuol dire che, data ad esempio la funzione proposizionale 'se x é un uomo, x é mortale' , la teoria dei tipi dà regole per i valori che x può ammettere. Ad esempio, da tale funzione é legittimo inferire la proposizione 'se Socrate é un uomo, Socrate é mortale' , ma non 'se la legge di contraddizione é un uomo, allora la legge di contraddizione é mortale' : quest'ultimo é solamente un gruppo di parole scevro di senso. Questo implica che 'Socrate' e 'la legge di contraddizione' appartengano a tipi diversi tra loro.
In tale contesto si colloca il famoso 'paradosso del barbiere', consistente in questo enunciato: in un paese dove tutti gli uomini sono rasati, esiste un solo barbiere il quale rade tutti gli uomini che non si radono da soli. Ma allora, chi rade il barbiere? Analizzando il problema con la teoria degli insiemi, è chiaro che nel paese esiste l'insieme degli uomini che si radono da soli e quello degli uomini che si fanno radere. Il barbiere si rade da solo? Impossibile, perchè il barbiere rade tutti gli uomini che non si radono da soli! Qualcun altro lo rade? No, perchè il barbiere rade tutti gli uomini che non si radono da soli! Ci troviamo di fronte ad un paradosso. Secondo Russell, per superarlo, bisogna correggere la nostra convinzione (errata) che per ogni proprietà debba per forza esistere un insieme: in qualche caso non si forma nessun insieme coerente.
"Non possiamo prendere le classi nel puro senso estensivo, semplicemente come mucchi o agglomerati. Se tentassinmo di farlo, troveremmo incomprenisibile come possa esistere una classe come la classe-nulla, che non ha membri affatto e non può essere considerata un «un mucchio»; troveremmo anche difficilissimo capire come una classe di un solo membro non sia identica a quel membro stesso."
 |
|
| Appunti Fisica |  |
| Tesine Statistica |  |
| Lezioni Geografia |  |