 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1348 | Gradito: |
Leggi anche appunti:Le geometrie non euclideeLe geometrie non euclidee Il problema delle geometrie non euclidee e la rivoluzione DerivataDERIVATA ( Dal latino : derivare = de - da , rivus -- ruscello , quindi La legge di hardy - weinbergLA LEGGE DI HARDY - WEINBERG Nel 1908 G. H. Hardy e W. Weinberg definirono |
 |
 |
Relazioni fra le funzioni goniometriche
Fra le funzioni goniometriche esistono delle relazioni: Abbiamo visto in precedenza che:
![]() e
e
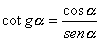
Il seno e il coseno possono essere espressi l'uno in funzione dell'altro dall'uguaglianza
![]()
Quindi
![]()
e
![]()
Risolvendo il sistema
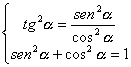 rispetto a seno e coseno, si trovano le seguenti relazioni:
rispetto a seno e coseno, si trovano le seguenti relazioni:
![]()
![]()
Ora siamo in grado di determinare i valori di
tutte le funzioni goniometriche, noto quello di una di esse e il quadrante in
cui si trova l'angolo.
Esercizio1
Dato sen![]() =3/4 e sapendo che l'angolo si trova nel I quadrante, determinare il valore di
tutte le altre funzioni goniometriche.
=3/4 e sapendo che l'angolo si trova nel I quadrante, determinare il valore di
tutte le altre funzioni goniometriche.
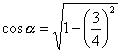 =
=![]() =
=![]()
 |
| Appunti su: |
|
| Appunti Geografia |  |
| Tesine Statistica |  |
| Lezioni Fisica |  |