La sezione aurea in geometria
La
sezione aurea è spesso messa in relazione, in geometria, con molte figure,
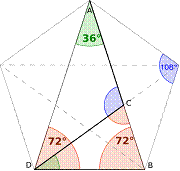
piane e solide, in particolare al pentagono regolare. Nel poligono legato tradizionalmente
alla scuola pitagorica, infatti, essa si riscontra nel rapporto fra la
diagonale e il lato. Nel decagono poi esprime il rapporto fra la misura del raggio
della circonferenza circoscritta e del lato; per quanto riguarda la geometria
solida il numero d'oro si lega al dodecaedro, il poligono a dodici pentagoni, e
all'icosaedro, entrambi solidi
platonici.
Rettangolo
aureo e triangolo aureo.
Esistono
due poligoni in cui la presenza di Φ nel rapporto fra i loro lati ha fatto
sì che venissero definiti "aurei". Il primo è il "rettangolo aureo", in cui il
rapporto fra base e altezza è uguale al rapporto aureo;
il secondo è il "triangolo aureo" in cui Φ è dato dal rapporto tra il lato
obliquo e la
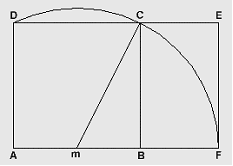
Costruzione del rettangolo
aureo.
|
|
base.
La spirale aurea.


La
conchiglia del Nautilus segue la curva della
spirale aurea: il
rapporto tra il diametro di una spira e quello della precedente è uguale a
|
|
Se all'interno del rettangolo aureo si disegna
un quadrato con lato uguale al lato minore del rettangolo, anche il rettangolo
differenza è un rettangolo aureo. Ripetendo l'operazione, si ottiene una
sequenza infinita di quadrati e rettangoli aurei. Se si traccia, poi, attraverso
questi quadrati, una serie di archi circolari che hanno come raggio i lati dei
quadrati stessi, la curva che ne consegue è la cosiddetta spirale aurea.
Quest'ultima è un elemento che si trova spesso anche in natura, ad esempio nella
conformazione della conchiglia del Nautilus.