 |
|
| Appunti scientifiche |
|
|
|
| Appunti scientifiche |
|
| Visite: 1625 | Gradito: |   [ Picolo appunti ] |
Leggi anche appunti:Lo studio di funzioniLO STUDIO DI FUNZIONI FUNZIONE : Una relazione fra due insiemi A Formule matematicaFormule matematica Geometria Analitica La retta: » equazione Dante e la matematicaDANTE E LA MATEMATICA Dopo gli anni '90 del XIII secolo, Dante si dedica |
 |
 |
EQUAZIONE DIFFERENZIALE NON OMOGENEA
(1)
|
TERMINE NOTO f(x) |
CONDIZIONI |
INTEGRALE PARTICOLARE |
N O T E |
|
POLINOMIO DI GRADO n |
|
Polinomio di grado n = |
|
|
|
Polinomio di grado n+1 = |
|
|
|
|
Polinomio di grado n+2 = N.B SI INTEGRA 2 VOLTE SUCCESSIVAMENTE |
|
|
|
|
Se |
|
|
|
Se |
|
|
|
|
Se |
|
|
|
|
dove f(x) è un polinomio di grado n |
Se |
|
|
|
Se |
|
|
|
|
Se |
|
|
|
|
|
In questo caso si applica il principio di sovrapposizione delle soluzioni determinando 2 integrali particolari, con riferimento al caso precedente
|
|
|
|
|
Se |
|
|
|
Se |
x( |
|
|
|
|
Se |
con A(x) e B(x) opportuni polinomi di grado non superiore al maggiore fra i gradi di P(x) e Q(x). |
|
|
Se |
x[ |
|
|
NOTE:
L'integrale generale di una equazione differenziale, non
omogenea del 2° ordine è dato dall'integrale generale 
della equazioni
omogenea associata;
e da un integrale particolare q(x) della non omogenea. Cioè
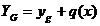
Le costanti che compaiono devono essere determinate: si calcolano le derivate 1a e 2a dell'integrale particolare. Si sostituiscono alle derivate trovate nell'equazione differenziale completa e si applica il principio di identità dei polinomi.
|
| Appunti su: |
|
| Appunti Statistica |  |
| Tesine Fisica |  |
| Lezioni Geografia |  |
non è radice delle equazione caratteristica
e 
non è radice della equazione caratteristica
non è radice della equazione caratteristica