 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2343 | Gradito: |
Leggi anche appunti:Concorrenza monopolisticaConcorrenza monopolistica Le condizioni che definiscono l'esistenza di un Stima fondi rusticiSTIMA FONDI RUSTICI La differenza tra una stima analitica di un fondo rustico I contratti nel commercio marittimoI contratti nel commercio marittimo Rischi e responsabilità Il |
 |
 |
Il teorema «generale» di immunizzazione per shift additivi
L'impostazione di Redington (riformulata nel TEOREMA 3) fornisce una terna di condizioni per l'immunizzazione del valore di un portafoglio, definito a copertura di un flusso di impegni (uscite multiple), rispetto a shift additivi infinitesimi della struttura dei rendimenti; il TEOREMA 3 non può essere considerato una generalizzazione propria, al caso di uscite multiple, del «teorema di immunizzazione» di Fisher e Weil (enunciato, in forma equivalente all'originaria, nel TEOREMA l), che come visto è valido nel caso di singolo impegno, ma per shift di ampiezza finita.
La caratterizzazione di un teorema generale (valido per uscite multiple e shift additivi «finiti») può essere impostata osservando che il problema di copertura di un flusso di impegni y è «scomponibile» in tante operazioni di copertura, ognuna definita in riferimento ad una singola posta di y (e quindi analizzabile nello schema di Fisher e Weil).
Su questa linea, condizione sufficiente per l'immunizzazione è che il portafoglio di copertura x possa essere scomposto in «m portafogli», ciascuno dei quali immunizzi «separatamente» uno degli m impegni del flusso y, in modo conforme alle condizioni del TEOREMA 1.
È possibile formulare il criterio della scomponibilità enunciando quello che può essere considerato il teorema «generale» di immunizzazione per shift additivi (il teorema va attribuito a Fong e Vasicek).
TEOREMA 4
Sia:
(t,s) l'intensità istantanea di interesse corrispondente alla struttura a termine osservata al tempo t,
x ed y due flussi ad elementi non negativi, con scadenze
tl, t2, , tm ( t < tl ≤ t2 ≤ . ≤ tm).
Se la curva dei rendimenti subisce nell'istante t+, immediatamente successivo a t, uno shift additivo di ampiezza aleatoria, allora il valore post-shift del flusso x sarà non-minore del valore post-shift di y
W(t+,x) ≥ W(t+,y) ,
se e solo se valgono le seguenti tre condizioni:
W(t,x) = W(t,y)
D(t,x) = D(t,y)
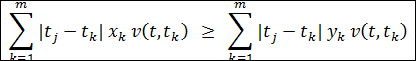
( j = 1, 2, ., m ).
Il TEOREMA 4 ricalca la struttura dei teoremi originari dell'immunizzazione classica; richiede che i flussi di copertura x e di indebitamento y soddisfino il vincolo di bilancio e condizioni sui livelli di dispersione temporale dei «valori attuali» delle poste. Più precisamente, le condizioni (3) costituiscono i cosiddetti vincoli «MAD» (Mean Absolute Deviation) e possono essere lette come richiesta che il flusso di copertura x sia più disperso nel tempo del flusso delle passività y, essendo la dispersione misurata in termini di «dispersione media assoluta» (momento assoluto del primo ordine) rispetto a ciascun punto di ascissa (scadenza) tj (con j = 1, 2, ., m ) con pesi i valori attuali relativi dei singoli pagamenti.
Con riferimento alla linea dimostrativa, è agevole definire in modo conclusivo il ruolo del teorema «generale»di immunizzazione nell'ambito della teoria classica.
Innanzitutto, va precisato che il TEOREMA 4 è valido non soltanto per shift additivi, ma più in generale per shift «convessi», e che le condizioni (1), (2) e (3) sono necessarie (e sufficienti) per l'immunizzazione da shift convessi.
Inoltre, utilizzando il «teorema di equivalenza», si dimostra che il teorema di Redington è contenuto nel TEOREMA 4; è agevole dimostrare che anche l'immunizzazione nel senso di Fisher e Weil è garantita dalle condizioni del teorema generale: infatti, se si ipotizza un flusso di passività y ridotto ad un'unica uscita L all'istante H (coincidente con uno dei tempi tk), si vede facilmente che i vincoli di tipo MAD (3) sono sempre soddisfatti purché siano soddisfatti il vincolo di bilancio e la condizione di duration.
 |
| Appunti su: https:wwwappuntimaniacomscientificheeconomiail-teorema-generale-di-immuniz95php, |
|
| Appunti Marketing |  |
| Tesine costruzione |  |
| Lezioni Agricoltura agraria |  |