 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1975 | Gradito: |
Leggi anche appunti:Tecnica: l'energia nucleareTECNICA: L'ENERGIA NUCLEARE L'energia nucleare è una forma d'energia Elettroliti, non-elettroliti e grado di dissociazioneElettroliti, non-elettroliti e grado di dissociazione Le sostanze che si Nomenclatura composti inorganiciNomenclatura composti inorganici Tabella con i primi 100 elementi chimici (Z |
 |
 |
GLI INTEGRALI DEFINITI
Prima
di parlare di integrali definiti, dobbiamo dare la definizione di integrale
indefinito. Per dare la definizione di quest'ultimo introduco il concetto di
primitiva di una funzione. Data una funzione ![]() continua e derivabile in un intervallo [a;b],
si dice che una funzione
continua e derivabile in un intervallo [a;b],
si dice che una funzione ![]() è una primitiva della funzione
è una primitiva della funzione ![]() ,
se la derivata prima della funzione
,
se la derivata prima della funzione ![]() è uguale alla funzione iniziale. Se ad esempio
abbiamo:
è uguale alla funzione iniziale. Se ad esempio
abbiamo:
![]()
![]()
![]()
la
funzione ![]() è una primitiva della funzione iniziale poiché
la sua derivata è uguale alla funzione originale. Le primitive di una funzione
si possono indicare
è una primitiva della funzione iniziale poiché
la sua derivata è uguale alla funzione originale. Le primitive di una funzione
si possono indicare ![]() e quindi sono infinite. La totalità delle
primitive di 1 funzione si chiama integrale indefinito della funzione
e quindi sono infinite. La totalità delle
primitive di 1 funzione si chiama integrale indefinito della funzione ![]() e si indica con
e si indica con
![]()
Per l'integrale sia indefinito, che definito valgono queste 2 proprietà:
L'integrale del prodotto di una costante per una funzione è uguale al prodotto della costante per l'integrale della funzione.
![]()
L'integrale della somma di più funzioni è uguale alla somma degli integrali delle singole funzioni.
![]()
Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell'integrale definito. Il problema del calcolo dell'area di 1 trapezoide, cioè una superficie piana delimitata da contorni curvilinei, ha portato al concetto di questo tipo di integrale.
Data
una funzione ![]() continua e positiva in un intervallo chiuso
[a;b], per calcolare l'area di un trapezoide si divide l'intervallo [a;b] in un
certo numero di parti h tutti uguali e di ampiezza
continua e positiva in un intervallo chiuso
[a;b], per calcolare l'area di un trapezoide si divide l'intervallo [a;b] in un
certo numero di parti h tutti uguali e di ampiezza ![]() ; dopo si costruiscono dei rettangoli
inscritti alla funzione per ogni segmento di base h e di altezza il valore
minimo della funzione che assume in quell'intervallo, indicando quest'ultimo
con mi; si costruiscono successivamente dei rettangoli circoscritti
alla funzione con base h e altezza il valore massimo che la funzione assume in
quel'intervallo, indicando quest'ultimo con Mi.
; dopo si costruiscono dei rettangoli
inscritti alla funzione per ogni segmento di base h e di altezza il valore
minimo della funzione che assume in quell'intervallo, indicando quest'ultimo
con mi; si costruiscono successivamente dei rettangoli circoscritti
alla funzione con base h e altezza il valore massimo che la funzione assume in
quel'intervallo, indicando quest'ultimo con Mi.
Se noi consideriamo le aree dei rettangoli inscritti avremo che:
h·mi = Area di 1 rettangolo
sn = somma delle aree dei rettangoli inscritti
![]()
Se consideriamo invece le aree dei rettangoli circoscritti alla funzione, avremo che:
h·Mi = Area di 1 rettangolo
Sn = somma delle aree dei rettangoli circoscritti
![]()
Grafico: y
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() N
N
Mi
M
mi h h h h h h h h x
![]()
![]() a x x x x x x x b
a x x x x x x x b
Comune alle 2 successioni sn e Sn ci sarà S:
sn < S < Sn
Ma sia sn sia Sn sono delle successioni convergenti, avendo lo stesso limite, e convergono verso uno stesso numero cioè S.
![]()
Tale limite comune S rappresenta l'area del Trapezoide. Pertanto possiamo definir che:
Data una funzione ![]() continua in [a;b] , si chiama integrale
definito esteso all'intervallo [a;b] il valore comune del limite per
continua in [a;b] , si chiama integrale
definito esteso all'intervallo [a;b] il valore comune del limite per ![]() delle due successioni sn e Sn.
Questo valore viene indicato
delle due successioni sn e Sn.
Questo valore viene indicato
![]()
Il numero a si chiama estremo inferiore, il
numero b estremo superiore, mentre la funzione ![]() si chiama funzione integranda.
si chiama funzione integranda.
Il simbolo che indica l'integrale ( rappresenta una S allungata per ricordare che. nella rappresentazione grafica, ad un integrale corrisponde una somma di aree.
Quindi mentre l'integrale definito è un numero, quello indefinito p una somma di primitive.
Per l'integrale definito valgono alcune proprietà, oltre le 2 già dell'integrale indefinito:
se b > a ![]() ; se a > b
; se a > b ![]()
quindi ![]()
se a = b
![]()
![]() [a;b]
[a;b]
se
c'e un punto ![]()
allora vale la proprietà di additività e quindi:
![]()
![]() , che rappresenta l'area di 1 rettangolo
, che rappresenta l'area di 1 rettangolo
![]()
E' possibile enunciare il teorema fondamentale dell'integrale definito, il teorema di Torricelli:
Se
una funzione ![]() è continua in
è continua in ![]() ,
la corrispondente funzione integrale
,
la corrispondente funzione integrale![]() è derivabile per tutte le
è derivabile per tutte le ![]() di
di ![]() (è una funzione perché dipende dall'estremo
superiore che varia nell'intervallo
(è una funzione perché dipende dall'estremo
superiore che varia nell'intervallo![]() ),
cioè:
),
cioè:
![]()
si dimostra che:
![]()
Questa la dimostrazione:
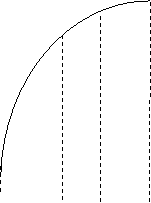
Data
una funzione ![]() continua in
continua in![]() esiste
esiste ![]()
![]() y
y
![]()
![]()
![]() x
x
a x x+h b
Se noi incrementiamo la x con x + h, avremo che
![]()
![]()
Se adesso ci calcoliamo l'incremento della nostra funzione integrale avremo:
![]()
Per la proprietà di additività possiamo anche scrivere
![]()
Se applichiamo il teorema della media:
![]() e quindi
e quindi ![]()
e se b - a costituisce l'ampiezza dell'intervallo di integrazione, avremo che
![]()
quindi
![]()
allora possiamo scrivere che:
![]()
Se dividiamo entrambi i membri per h, otteniamo che
![]()
dove il primo membro rappresenta il rapporto incrementale della funzione integrale.
Se poniamo il limite per h che tende a 0 di entrambi membri, avremo:
![]()
Il
primo membro non rappresenta altro che la derivata della funzione integrale (![]() ,
mentre il secondo limite per
,
mentre il secondo limite per ![]() di
di ![]() ,
al tendere a 0 di h, il punto c che è interno all'intervallo
,
al tendere a 0 di h, il punto c che è interno all'intervallo ![]() ,
tenderà a
,
tenderà a ![]()
Quindi si verifica l'enunciato del teorema:
![]()
Da questo teorema fondamentale del calcolo integrale è possibile dedurre la formula fondamentale del calcolo integrale, in base alla quale l'integrale definito è uguale alla differenza dei valori che una qualsiasi primitiva G(x) della funzione integranda f(x) assume all'estremo superiore e inferiore nell'intervallo [a;b].
![]()
Si può benissimo dimostrare anche questa formula chiamata di Newton - Leibniz.
Dato che![]() e
e ![]()
possiamo dire che
![]()
dove per ![]() si indica una generica primitiva della
funzione
si indica una generica primitiva della
funzione ![]()
se poniamo ![]()
![]() quindi
quindi ![]()
Sostituendo nell'equazione di prima, abbiamo che
![]()
se poi poniamo ![]() e sostituiamo, abbiamo la formula finale:
e sostituiamo, abbiamo la formula finale:
![]()
 |
| Appunti su: |
|
| Appunti Biologia |  |
| Tesine Geografia |  |
| Lezioni Ingegneria tecnico |  |