 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2587 | Gradito: |
Leggi anche appunti:Elettrolisi di sali fusiElettrolisi di sali fusi Se immergiamo due elettrodi collegati ad un generatore Variabili determinate in spettrometria di assorbimento molecolareVariabili determinate in spettrometria di assorbimento molecolare Le determinazioni Nomenclatura composti inorganiciNomenclatura composti inorganici Tabella con i primi 100 elementi chimici (Z |
 |
 |
Caratterizzazione dell'Attacco in KOH
In
questo lavoro di tesi è stato caratterizzato l'attacco del silicio con
orientazione <110> in soluzioni binarie ![]() e ternarie
e ternarie ![]() .
.
É stato investigato il cambiamento della velocità di attacco al variare della concentrazione di KOH nella soluzione di attacco e della temperatura per entrambi i sistemi considerati.
Per
le soluzioni ternarie ![]() non è stata
considerata la variazione della velocità di attacco con la concentrazione di
isopropanolo: sono stati condotti attacchi in soluzioni sature in isopropanolo.
La solubilità dell' isopropanolo nelle soluzioni di
non è stata
considerata la variazione della velocità di attacco con la concentrazione di
isopropanolo: sono stati condotti attacchi in soluzioni sature in isopropanolo.
La solubilità dell' isopropanolo nelle soluzioni di ![]() è infatti molto bassa, circa 3% in peso (%wt.)
ad
è infatti molto bassa, circa 3% in peso (%wt.)
ad ![]() (Bibl. 5): aggiungendo isopropanolo ad una
soluzione di
(Bibl. 5): aggiungendo isopropanolo ad una
soluzione di ![]() si ottengono quindi due fasi: isopropanolo
puro e la soluzione
si ottengono quindi due fasi: isopropanolo
puro e la soluzione ![]() , satura in isopropanolo. Questo garantisce la stabilità
della concentrazione di isopropanolo in soluzione, e permette quindi di
trascurare la volatilità dell'alcole.
, satura in isopropanolo. Questo garantisce la stabilità
della concentrazione di isopropanolo in soluzione, e permette quindi di
trascurare la volatilità dell'alcole.
Sono stati condotti un totale di 20 attacchi, i cui parametri e risultati sono presentati nella Tab. I:

Tab. I
Passi di processo
Negli
esperimenti sono stati impiegati wafer di Si Czochralski da 3 pollici di tipo n
con orientazione ![]() , spessore 356-406
, spessore 356-406![]() e resistenza per quadro 1-20
e resistenza per quadro 1-20![]() .
.
Per il
mascheramento è stato utilizzato ![]() cresciuto
termicamente: è stato infatti mostrato (2) che la velocità di attacco
dell'ossido termico è minore di quella dell'
cresciuto
termicamente: è stato infatti mostrato (2) che la velocità di attacco
dell'ossido termico è minore di quella dell'![]() depositato per CVD.
depositato per CVD.
Preparazione dei Campioni
Dopo il LAVAGGIO IN ULTRASUONI, il wafer viene sottoposto ad OSSIDAZIONE TERMICA DRY o WET.
I campioni numero 401,
402, 403, 412, 413, 434, 439, 441, 445, 452 sono stati ricavati da un wafer
sottoposto ad ossidazione wet alla temperatura di 950°C per 30 minuti: lo
strato di ![]() cresciuto è spesso circa 200nm.
cresciuto è spesso circa 200nm.
I campioni numero 455,
456, 457, 460, 466, 468, 469, 472, 481 sono stati ricavati da un wafer
sottoposto ad ossidazione dry alla temperatura di 1000°C per 40 minuti: lo
strato di ![]() cresciuto è spesso circa 60nm.
cresciuto è spesso circa 60nm.
Dopo l'ossidazione, il wafer deve essere tagliato per ricavarne campioni di dimensioni opportune.
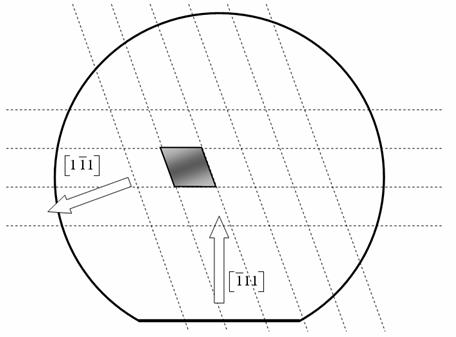
Fig. 1: Linee di taglio rispetto al flat del wafer del Si [110] tipo n.
Taglio dei Campioni
Il taglio si esegue mediante una piccola incisione del wafer con una punta diamantata, seguita da forzatura per spezzare il cristallo lungo la linea incisa.
Questo tipo di
taglio ha successo se le linee incise sono allineate con i piani ![]() , ortogonali al substrato (
, ortogonali al substrato (![]() ,
, ![]() ,
, ![]() e
e ![]() : vedi par. I), che offrono maggiore resistenza agli stress:
i campioni ricavati sono dunque romboidali.
: vedi par. I), che offrono maggiore resistenza agli stress:
i campioni ricavati sono dunque romboidali.
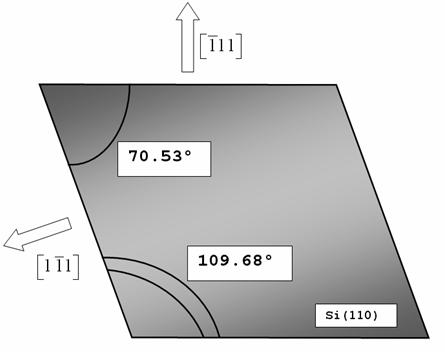
Fig. 2: Forma di un campione ricavato dal wafer con
orientazione ![]() .
.
Litografia
Il campione di Si così ottenuto viene sottoposto a LAVAGGIO IN ULTRASUONI, dopodiché vi viene steso il resist.
Il campione numero 401 è stato litografato con FOTOLITOGRAFIA, mentre tutti gli altri con EBL.
Sui campioni 402, 403, 412, 413 è stato steso il MONOLAYER 6%, e sono stati scritti a bassa risoluzione, ad ingrandimento 40X.
Sui campioni 434, 439, 441, 445, 452, 455, 456, 457, 460, 466, 472 è stato steso il BILAYER 3%, e sono stati scritti ad alta risoluzione, ad ingrandimento 400X.
Sui campioni 468, 469, 481 è stato steso il BILAYER 1.5%, e sono stati scritti ad alta risoluzione, ad ingrandimento 400X..
Le geometrie scritte consistono in
gruppi di rettangoli con un lato molto maggiore dell'altro, allineati in modo
tale che il lato maggiore sia parallelo ad uno dei piani ![]() ortogonali al
substrato (Fig. 3).
ortogonali al
substrato (Fig. 3).
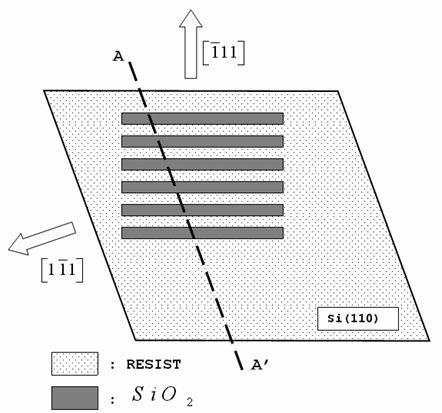
Fig. 3: Rappresentazione schematica della vista dall'alto di un
campione dopo il passo di litografia: le aree rettangolari più scure sono
quelle in cui il resist è stato impresso e sviluppato, lasciando scoperto l'![]()

Tab. II
Attacco dell'Ossido
L'ossido
di silicio rimasto esposto dopo il passo di litografia (Fig. 3) viene
sottoposto ad un attacco umido isotropo a temperatura ambiente in una soluzione
BHF (Buffered HF), con la seguente
composizione chimica: 34.6% wt. di floruro di ammonio (![]() ), 13.8% wt. di acido fluoridrico (HF) al 48%, 51.7% wt. di
acqua deionizzata.
), 13.8% wt. di acido fluoridrico (HF) al 48%, 51.7% wt. di
acqua deionizzata.
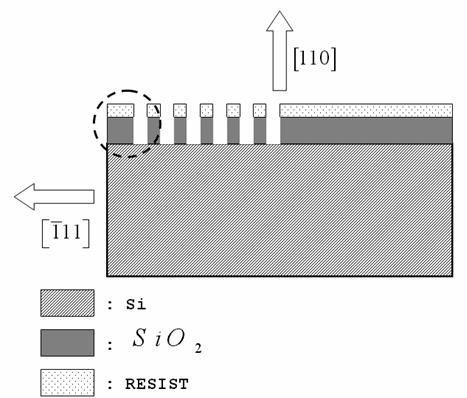
Fig. 4: Vista della sezione A-A' della Fig. 3 di un campione dopo l'attacco BHF.
La
velocità di attacco dell'ossido in tale soluzione è di circa ![]() : il tempo di attacco scelto è stato dunque 5 minuti per i
campioni con ossido spesso, e 75 secondi per quelli con ossido sottile (si veda
la Tab. II).
: il tempo di attacco scelto è stato dunque 5 minuti per i
campioni con ossido spesso, e 75 secondi per quelli con ossido sottile (si veda
la Tab. II).
Questi tempi di attacco non devono però essere presi rigorosamente in considerazione, poiché gli attacchi sono stati portati a temperatura ambiente senza termostatare la soluzione (la cui velocità di attacco in funzione della temperatura ha un andamento tipo Arrhenius), ed il ripetuto uso della soluzione ne cambia il comportamento in termini di velocità di attacco.
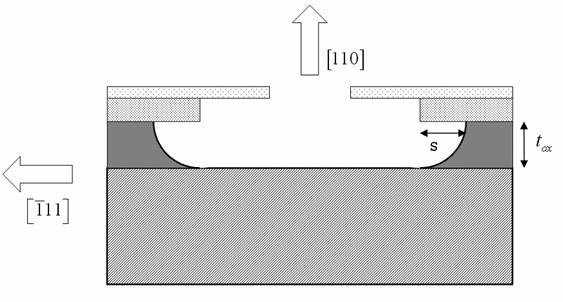
Fig. 5: Rappresentazione dettagliata dell'area inscritta nel cerchio tratteggiato in Fig. 3, nel caso che sul campione sia stato steso un bilayer di resist.
Dalla Fig. 5 si nota come, per l'isotropia
dell'attacco BHF, il sottoattacco sia pari allo spessore di ![]() cresciuto sul
campione:
cresciuto sul
campione: ![]() . Questa è una condizione ideale, in cui si suppone che il
tempo di attacco sia esattamente pari a quello necessario a consumare lo strato
di ossido: infatti, dal momento che non è stata effettuata una calibrazione
rigorosa dei tempi di attacco, si attacca in genere per un tempo superiore a
quello minimo (overetch), per cui si
ha
. Questa è una condizione ideale, in cui si suppone che il
tempo di attacco sia esattamente pari a quello necessario a consumare lo strato
di ossido: infatti, dal momento che non è stata effettuata una calibrazione
rigorosa dei tempi di attacco, si attacca in genere per un tempo superiore a
quello minimo (overetch), per cui si
ha ![]() .
.
S limita inferiormente la minima dimensione delle geometrie che possono essere ottenute con questo processo: per questo (ma anche per un'altra motivazione più determinante, che sarà chiarita nel par. 1.6), è stato deciso di ridurre le dimensioni dell'ossido termico cresciuto da 200nm a 60nm.
Attacco in KOH
Dopo l'attacco in BHF, viene effettuato lo strip del resist, immergendo il campione in acetone e risciacquandolo in IPA (Fig. 6)
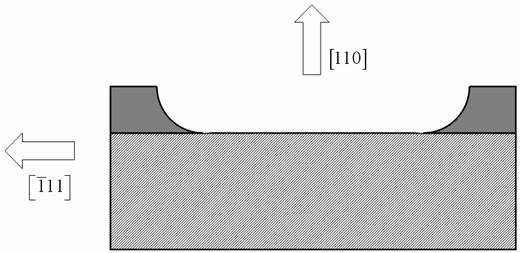
Fig. 6: Rappresentazione della sezione del campione dopo lo strip del resist.
Le soluzioni di attacco sono state preparate con idrossido di potassio di PM=56.11, isopropanolo di PM=60.097 e acqua deionizzata del deionizzatore Milli-Q (ACADEMIC).
Gli attacchi alla temperatura di 0°C sono stati condotti in un bagno termico costituito da acqua deionizzata alla temperatura di transizione di fase solido-liquido, mediante il sistema illustrato in Fig. 7.
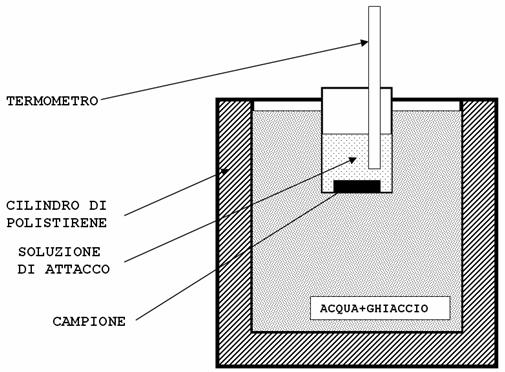
Fig. 7: Sistema usato per gli attacchi a 0°C.
Gli attacchi a temperatura 28°C, 38°C e 45°C sono stati condotti nel bagno termostato HAAKE DC50 (ENCO).
Allineamento
Su
un wafer ![]() , la velocità di sottoattacco laterale aumenta molto
velocemente in funzione del disallineamento angolare nell'intorno dei suoi
minimi assoluti sui piani
, la velocità di sottoattacco laterale aumenta molto
velocemente in funzione del disallineamento angolare nell'intorno dei suoi
minimi assoluti sui piani ![]() (Fig. 8): per
applicazioni in cui sono importanti alti rapporti di aspetto (AR), è quindi
cruciale un preciso allineamento angolare.
(Fig. 8): per
applicazioni in cui sono importanti alti rapporti di aspetto (AR), è quindi
cruciale un preciso allineamento angolare.
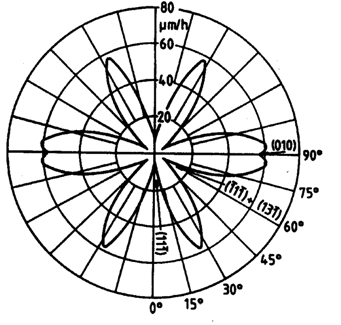
Fig. 8: Velocità di sottoattacco in funzione dell'orientazione su un
wafer di Si ![]() attaccato in una
soluzione al 50% wt di KOH, alla temperatura di 78°C (Bibl. 2).
attaccato in una
soluzione al 50% wt di KOH, alla temperatura di 78°C (Bibl. 2).
In
questo lavoro di tesi non è stato giudicato importante raggiungere un alto AR.
Lo scopo della caratterizzazione dell'attacco in KOH su Si ![]() è stato infatti quello
di ottenere scavi profondi qualche decina di nm: l'aumento della larghezza
dello scavo dovuto al basso AR è stato quindi considerato tollerabile, perché
dell'ordine del nm (si deve comunque notare che il sistema di rotazione
meccanica del SEM ha una risoluzione angolare troppo bassa, pari a 0.1s, per
rendere possibile un allineamento angolare fine).
è stato infatti quello
di ottenere scavi profondi qualche decina di nm: l'aumento della larghezza
dello scavo dovuto al basso AR è stato quindi considerato tollerabile, perché
dell'ordine del nm (si deve comunque notare che il sistema di rotazione
meccanica del SEM ha una risoluzione angolare troppo bassa, pari a 0.1s, per
rendere possibile un allineamento angolare fine).
L'allineamento
angolare delle strutture litografate è stato compiuto manualmente, allineandosi
ad ingrandimento 550X sul bordo del campione ortogonale alla direzione ![]() .
.
Perché questo processo potesse essere utilizzato per la fabbricazione di una giunzione tunnel (vedi cap. IV), era importante che permettesse di ottenere uno scavo con pareti e fondo quanto più possibile lisci.
L'irregolarità
delle pareti dello scavo è stata imputata all'irregolarità della maschera di ![]() : per minimizzarla si è quindi progressivamente aumentata la
risoluzione del processo litografico, passando dalla fotolitografia, all'EBL a
bassa risoluzione, a ad alta risoluzione, ed infine ad ultra alta risoluzione,
e si è diminuito lo spessore dell'ossido, da circa 200nm, a circa 60nm.
: per minimizzarla si è quindi progressivamente aumentata la
risoluzione del processo litografico, passando dalla fotolitografia, all'EBL a
bassa risoluzione, a ad alta risoluzione, ed infine ad ultra alta risoluzione,
e si è diminuito lo spessore dell'ossido, da circa 200nm, a circa 60nm.


Fig. 9: Riduzione dell'irregolarità delle pareti laterali dello scavo:
la foto di destra si riferisce al campione 413, che è stato litografato con EBL
a bassa risoluzione ed attaccato in una soluzione di ![]() al 50% wt. a 0°C per
60 minuti; la foto di sinistra si riferisce al campione 426, che è stato
attaccato nello stesso modo, ma litografato con EBL ad alta risoluzione
al 50% wt. a 0°C per
60 minuti; la foto di sinistra si riferisce al campione 426, che è stato
attaccato nello stesso modo, ma litografato con EBL ad alta risoluzione
Misura degli Spessori
Per
misurare la profondità degli scavi, il campione è stato tagliato con la punta
diamantata lungo il piano ![]() , in modo tale che la linea del taglio intersechi l'area
attaccata, come mostrato in Fig. 10.
, in modo tale che la linea del taglio intersechi l'area
attaccata, come mostrato in Fig. 10.
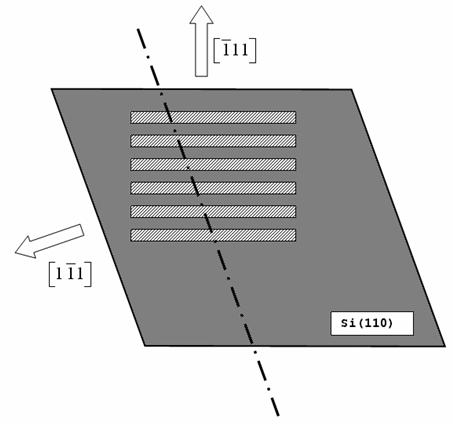
Fig. 10: Taglio del campione: la linea di taglio è rappresentata dalla linea tratto-punto.
A questo punto si è montato uno dei pezzi ottenuti sul portacampioni del SEM, che permette di vedere i campioni di taglio.
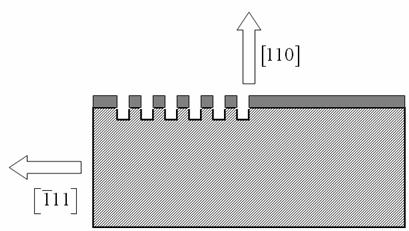
Fig. 11: Rappresentazione della sezione del campione alla fine del processo.
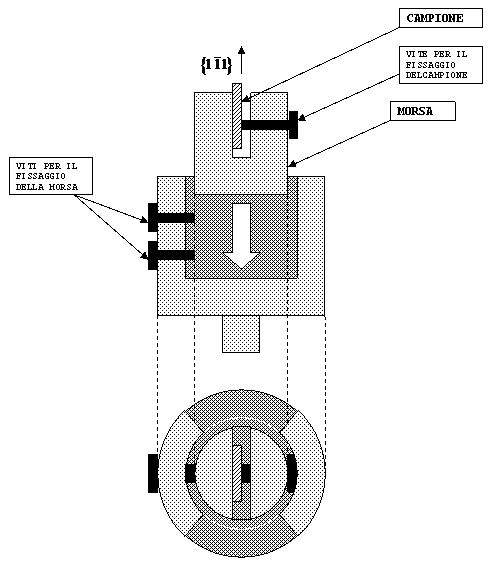
Fig. 12: Montaggio del campione sul portacampioni.
Riepilogo del Processo
I passi di processo possono essere cosi riassunti e schematizzati:
Ossidazione termica
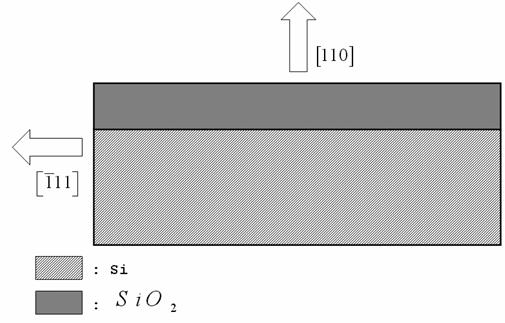
Litografia
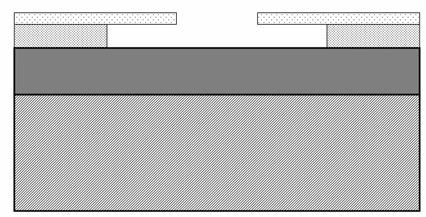
Attacco
dell'![]() in BHF
in BHF
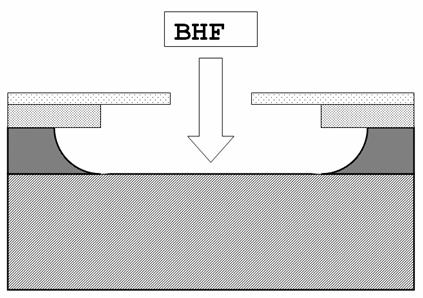
Strip del resist
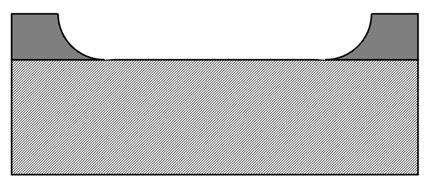
Attacco anisotropo del Si in KOH
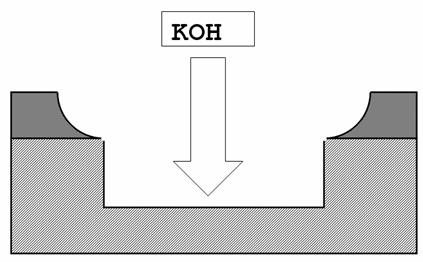
Il valor medio e la deviazione
standard delle velocità di attacco verticale nel substrato di Si ![]() che si sono ottenuti
in questo lavoro di tesi sono riportati in Tab. III
che si sono ottenuti
in questo lavoro di tesi sono riportati in Tab. III
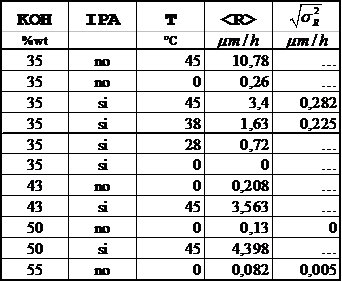
Tab. III
Dipendenza dalla Temperatura
La dipendenza dalla temperatura della
velocità di attacco verticale delle soluzioni ![]() e
e ![]() su un substrato
su un substrato ![]() è di tipo Arrhenius
(Bibl. 2):
è di tipo Arrhenius
(Bibl. 2):
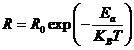
dove ![]() è la costante di
Boltzmann, e T la temperatura assoluta in Kelvin.
è la costante di
Boltzmann, e T la temperatura assoluta in Kelvin.
I valori per l'energia di attivazione ![]() ed il fattore
preesponenziale
ed il fattore
preesponenziale ![]() , che dipendono dalla composizione e dalla concentrazione
della soluzione di attacco, devono essere determinati con il fitting della sui dati sperimentali.
, che dipendono dalla composizione e dalla concentrazione
della soluzione di attacco, devono essere determinati con il fitting della sui dati sperimentali.
In questo lavoro di tesi sono stati
determinati i valori di ![]() ed
ed ![]() per la soluzione
per la soluzione ![]() 35%wt di KOH e per la
35%wt di KOH e per la ![]() 35%wt di KOH.
35%wt di KOH.
Attacco in ![]()
Per la soluzione ![]() 35%wt di KOH, sono
stati ottenuti i seguenti dati:
35%wt di KOH, sono
stati ottenuti i seguenti dati:

Tab. I
Effettuando il fitting
Levenberg-Marquardt della funzione sui dati della Tab. I, sono stati ottenuti i seguenti valori per i
parametri ![]() ed
ed ![]() :
:
![]()
![]()
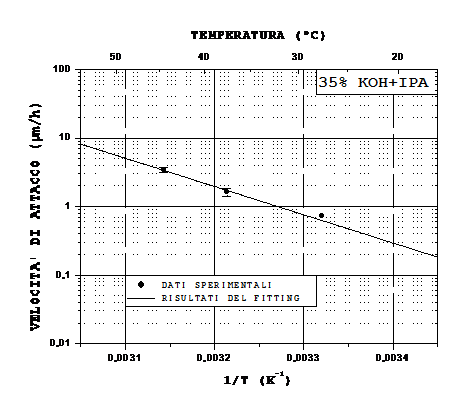
Fig. 1: Dipendenza dalla temperatura della velocità di attacco verticale
della soluzione ![]() al 35% wt di KOH su un substrato
al 35% wt di KOH su un substrato ![]() .
.
Attacco in ![]()
Per
la soluzione ![]() 35%wt di KOH, sono
stati ottenuti i seguenti dati:
35%wt di KOH, sono
stati ottenuti i seguenti dati:
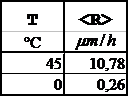
Tab. II
Per ottenere i
valori dei parametri ![]() ed
ed ![]() , non è stato in questo caso effettuato il fitting
Levenberg-Marquardt della funzione sui dati della Tab. II, ma semplicemente un fitting lineare della
funzione:
, non è stato in questo caso effettuato il fitting
Levenberg-Marquardt della funzione sui dati della Tab. II, ma semplicemente un fitting lineare della
funzione:
![]()
sui dati della Tab. III:

Tab. III
Che ha dato come risultato i valori di ![]() ed
ed ![]() , dai quali si è ottenuto:
, dai quali si è ottenuto:
![]()
![]()
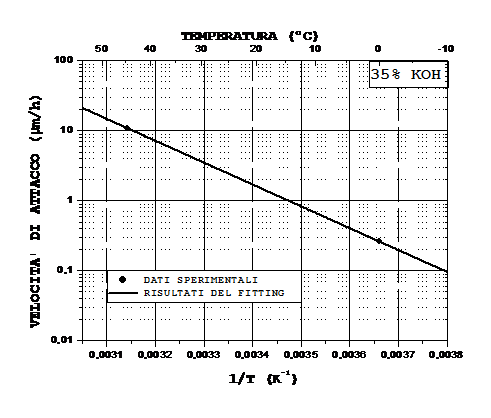
Fig. 2: Dipendenza dalla temperatura della velocità di attacco verticale
della soluzione ![]() al 35% wt di KOH su un substrato
al 35% wt di KOH su un substrato ![]() .
.
Conclusioni
È opportuno a questo punto giustificare la
scelta compiuta per il tipo di fitting da cui si sono ottenuti i valori di ![]() ed
ed ![]() .
.
Se si fosse deciso
di effettuare il fitting lineare della sui dati relativi agli attacchi compiuti nella soluzione ![]() 35%wt di KOH, si
sarebbe dovuto scartare il dato relativo a
35%wt di KOH, si
sarebbe dovuto scartare il dato relativo a ![]() , perché a tale temperatura si è ottenuto
, perché a tale temperatura si è ottenuto ![]() , e quindi
, e quindi ![]() .
.
Se, dall'alto lato, si fosse deciso di effettuare il fitting Levenberg-Marquardt della funzione sui dati della Tab. II, relativi agli attacchi compiuti nella
soluzione ![]() 35%wt di KOH,
l'affidabilità dei risultati ottenuti sarebbe stata minore, dal momento che si
hanno a disposizione dati relativi a due sole temperature.
35%wt di KOH,
l'affidabilità dei risultati ottenuti sarebbe stata minore, dal momento che si
hanno a disposizione dati relativi a due sole temperature.
Dai risultati ottenuti
nelle sezioni precedenti si ricava che, saturando in IPA una soluzione di KOH,
si riduce di circa il 90% la velocità di attacco verticale su substrati ![]() : in Fig. 1 viene presentato un grafico riassuntivo.
: in Fig. 1 viene presentato un grafico riassuntivo.
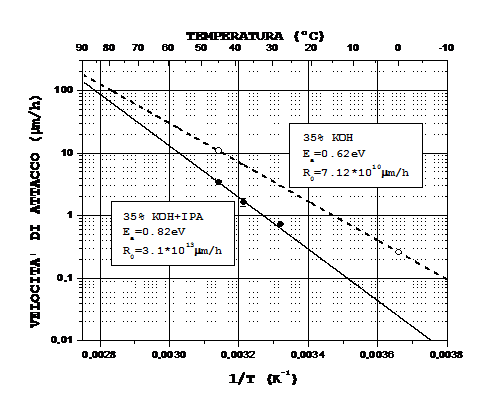
Fig. 1: Dipendenza dalla temperatura della
velocità di attacco verticale su un substrato ![]() .della soluzione
.della soluzione ![]() al 35% wt di KOH
(linea tratteggiata) e della soluzione
al 35% wt di KOH
(linea tratteggiata) e della soluzione ![]() al 35% wt di KOH
(linea continua).
al 35% wt di KOH
(linea continua).
Influenza di Composizione e Concentrazione
Si consideri l'equazione proposta da Seidel (Bibl. 2) per il calcolo della velocità di attacco:
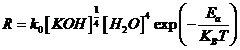
con:
![]()
![]()
![]() è la costante di
Boltzmann, e T la temperatura assoluta in Kelvin.
è la costante di
Boltzmann, e T la temperatura assoluta in Kelvin.
Le costanti ![]() e
e ![]() sono parametri il cui
valore deve essere ricavato con il fitting della sui dati raccolti.
sono parametri il cui
valore deve essere ricavato con il fitting della sui dati raccolti.
In base alla , la velocità di attacco è una funzione di tre variabili:
![]()
Per migliorare
l'affidabilità dei valori ottenuti dal fitting, è però necessario operare con
una funzione di una sola variabile: si deve quindi eliminare innanzitutto la
dipendenza dalla temperatura, fissandola ad un valore costante ![]() , ed esprimere poi la concentrazione molare di uno dei
componenti della soluzione in funzione di quella dell'altro.
, ed esprimere poi la concentrazione molare di uno dei
componenti della soluzione in funzione di quella dell'altro.
Considerando i dati relativi alla
velocità di attacco che sono stati raccolti in questo lavoro di tesi (Tab. III
del paragrafo 1), si è scelto come temperatura di attacco ![]() .
.
Si è infine scelto
di esprimere ![]() in funzione di
in funzione di ![]() :
:
![]()
La è quindi diventata:
![]()
Determinazione di ![]()
Si
esprima il volume totale della soluzione ![]() in funzione del numero
di moli di KOH e di
in funzione del numero
di moli di KOH e di![]() , e dei loro volumi molari parziali (Bibl. 11):
, e dei loro volumi molari parziali (Bibl. 11):
![]()
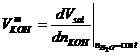
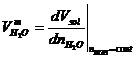
Il
procedimento per la determinazione di ![]() si fonda sull'assunzione
che sia lecito trascurare la dipendenza dei volumi molari parziali dalla
composizione della miscela, e dalla temperatura: si ottiene pertanto:
si fonda sull'assunzione
che sia lecito trascurare la dipendenza dei volumi molari parziali dalla
composizione della miscela, e dalla temperatura: si ottiene pertanto:
![]()
![]()
dove p è la pressione, che viene considerata costante e pari a 1atm.
Per ricavare ![]() alla temperature
d'interesse
alla temperature
d'interesse ![]() , si è misurato a temperatura ambiente (avendo assunto i
volumi molari parziali costanti con la temperatura) al variare della molalità del
KOH (ovvero il numero di moli di KOH per 1000g di
, si è misurato a temperatura ambiente (avendo assunto i
volumi molari parziali costanti con la temperatura) al variare della molalità del
KOH (ovvero il numero di moli di KOH per 1000g di ![]() ) il volume
) il volume ![]() di soluzioni tali che
la massa di
di soluzioni tali che
la massa di ![]() in esse presente fosse
costante e pari a 1000g, ottenendo i seguenti dati:
in esse presente fosse
costante e pari a 1000g, ottenendo i seguenti dati:
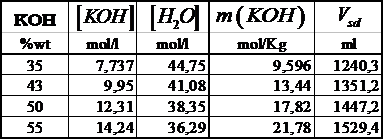
Tab II
Per il calcolo del numero di moli ci si è riferiti ai seguenti pesi molecolari:
![]()
![]()
Per le soluzioni considerate, ![]() può essere espresso come:
può essere espresso come:
![]()
con ![]() , la molalità del KOH.
, la molalità del KOH.
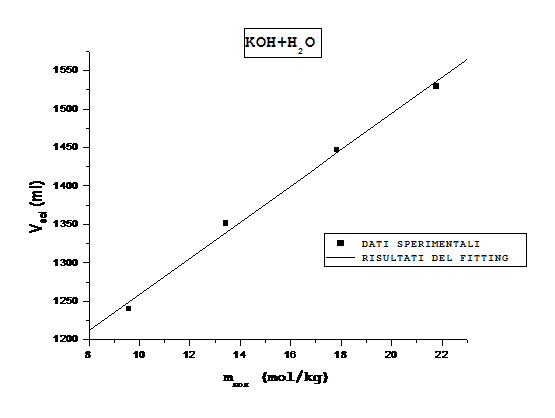
Fig. 1: ![]() in funzione della
molalità del
in funzione della
molalità del ![]() per soluzioni tali che
la massa di
per soluzioni tali che
la massa di ![]() in esse presente sia
costante e pari a 1000g
in esse presente sia
costante e pari a 1000g
Si
può quindi ricavare il valore di ![]() dal coefficiente
angolare della retta che interpola i dati (Fig. 1), ed usare la per ricavare
dal coefficiente
angolare della retta che interpola i dati (Fig. 1), ed usare la per ricavare ![]() , ottenendo:
, ottenendo:
![]()
![]()
A
questo punto si è in grado di esprimere la molarità di ![]() in funzione di quella
del KOH, infatti:
in funzione di quella
del KOH, infatti:

Considerando
soluzioni contenenti quantità di ![]() costanti e pari a
1000g, si potrà scrivere:
costanti e pari a
1000g, si potrà scrivere:
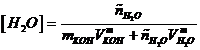
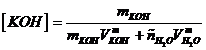
con ![]() .
.
Invertendo la , si ottiene ![]() in funzione di
in funzione di ![]() :
:
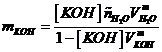
Sostituendo
la nella si ottiene finalmente ![]() in funzione di
in funzione di ![]() , ovvero la
, ovvero la ![]() :
:
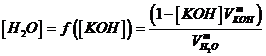
Fitting dell'Equazione di Seidel
Sostituendo la nella , si ottiene la forma esplicita della
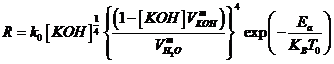
che, esplicitando le costanti, diventa:
![]()
I
dati relativi alla velocità di attacco di soluzioni di ![]() e KOH alla temperatura
e KOH alla temperatura
![]() raccolti in questo
lavoro di tesi sono:
raccolti in questo
lavoro di tesi sono:
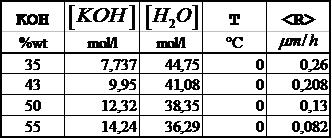
Tab. III
Effettuato il fitting Levemberg-Marquardt
della funzione sui dati della Tab. III sono stati ottenuti i seguenti valori per i
parametri empirici ![]() e
e ![]() :
:
![]()
![]()
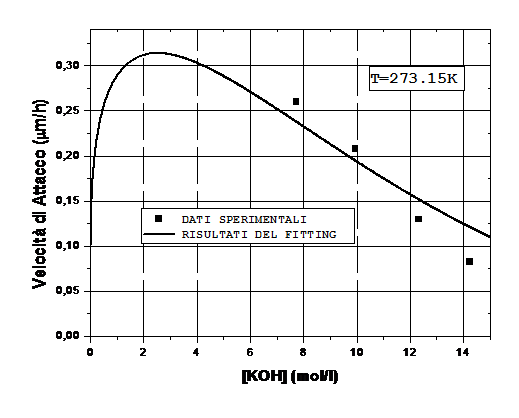
Fig. 2: Grafico dell' equazione di Seidel per ![]() e
e ![]() (linea continua), e
dati sperimentali (■).
(linea continua), e
dati sperimentali (■).
Rugosità superficiale
La rugosità delle superfici attaccate è un effetto di pseudomascheramento, ovvero è dovuta a un qualsiasi tipo di maschera non litografica che copre una parte della superficie in modo casuale e temporaneo.
Lo
pseudomascheramento è imputabile a molti possibili fattori: non uniformità
dell'ossido nativo; residui rimasti sulla superficie in seguito a processi di
pulizia; difetti nel cristallo di Si; bolle di ![]() che si accrescono sulla superficie durante
l'attacco; diffusione di
che si accrescono sulla superficie durante
l'attacco; diffusione di ![]() e
e ![]() verso la superficie, e di silicati via dalla
superficie; legami Si-H e Si-F presenti sulla superficie dopo un attacco in HF
e la pulizia in
verso la superficie, e di silicati via dalla
superficie; legami Si-H e Si-F presenti sulla superficie dopo un attacco in HF
e la pulizia in ![]() .
.
Il
primo studio sistematico e dettagliato della rugosità delle superfici attaccate
in KOH, dovuto a E. D. Palik (1991) (Bibl. 3), attribuisce la causa della
rugosità alla formazione di bolle di ![]() .
.
Durante l'attacco
si possono vedere bolle di ![]() che si accrescono sulla superficie del Si: per
tutto il tempo che queste bolle rimangono sulla superficie, dall'inizio del
loro accrescimento al momento del distacco, costituiscono una barriera per l'
che si accrescono sulla superficie del Si: per
tutto il tempo che queste bolle rimangono sulla superficie, dall'inizio del
loro accrescimento al momento del distacco, costituiscono una barriera per l'![]() e l'
e l'![]() .
.
Le caratteristiche delle bolle sono
funzione sia delle proprietà della soluzione d'attacco, come la molarità, la
tensione superficiale, la densità, la solubilità dell'![]() ,
la temperatura, il mescolamento (indipendentemente dal modo in cui esso sia
realizzato), che dalle proprietà della superficie, come le condizioni di
bagnabilità o la natura dei siti di nucleazione.
,
la temperatura, il mescolamento (indipendentemente dal modo in cui esso sia
realizzato), che dalle proprietà della superficie, come le condizioni di
bagnabilità o la natura dei siti di nucleazione.
In questo lavoro di tesi è stato osservato il comportamento della rugosità superficiale al variare della composizione soluzione di attacco, e della temperatura, ottenendo i risultati presentati in Fig. 1.
Come si vede,
aumentando la concentrazione di KOH e la temperatura, si ottiene un
miglioramento della superficie del fondo sia con soluzioni ![]() , che
, che ![]() .
.
A parità di concentrazione di KOH e temperatura, si ottiene la rugosità minore in soluzioni stura di IPA
![]()
![]()


 43%
43% 
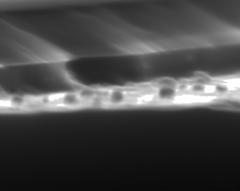 50%
50% 
 55%
55% 
T=0°C T=45°C
Fig. 1: Le superfici del fondo ottenute con attacchi a varie concentrazioni e temperature.
BIBLIOGRAFIA
"Silicon Anisotropic Etching in KOH-Isopropanol Etchant", Barycka, I. Zubel, Sensors and Actuators A 48, 229(1995)
"Anisotropic Etching of Crystalline Silicon in Alkaline Solutions: I.Orientation Dependance and Behaviour of Passivation Layers", H. Seidel, L. Csepregi, A. Heuberger, H. Baumgartel, J. Electrochem. Soc. 137, 3612 (1990)
"Etching roughness for (100) silicon surfaces in acqueous KOH", E. D. Palik, O. J. Glembocki, I. Heard, P. S. Burno, L. Tenerz, J. Appl. Phys. 70, 3291 (1991)
"Bulk Micromachining of Silicon" G. T. A. Kovaks, N. I. Maluf, K. E. Petersen, Proceedings of the IEEE 86, 1536 (1998)
"Silicon anisotropic etching in alkaline solutions II On the influence of anisotropy on the smoothness of etched surfaces" I. Zubel, Sensors and Actuators A 70, 260 (1998)
"AFM study of surface finish improvement by ultrasound in the anisotropic etching of Si <100> in KOH for micromachining applications" T. Baum, D. S. Schiffrin, J. Micromech. Microeng. 7, 338 (1997)
"Ellipsometric Study of Orientation Dependent Etching of Silicon in Aqueous KOH", E. D. Palik, V. M. Bermudez, O. J. Glembocki, J. Electrochem. Soc. 132, 871 (1985)
"Anisotropic etching of Silicon" K. E. Bean, Proc. IEEE 70, 420 (1982)
"Fabrication of novel three-dimensional microstructures by the anisotropic etching of (100) and (1100) silicon" E. Bassous, IEEE Trans. Electron. Devices, 25, 1178,(1978)
C. Kittel "Introduction to solid state physics", New York: Wiley, (1976), Cap. 1.
P. W. Atkins "Chemical Physics", Oxford University Press (1994), Cap. 7.
"A Raman Study of Etching Silicon in Aqueous KOH", E. D. Palik, H. F. Gray, P. B. Klein, J. Electrochem. Soc. 130, 956 (1983)
M. J. Madou "Fundamentals of Microfabrication" CRC Press (2002), Cap 4.
"Surface Morphology of p-Type (100) silicon etched in aqueous alkaline solution" P. M. M. C. Bressers, J. J. Kelly, J. G. E. Gardeniers, M. Elwenspoek J. Electrochem. Soc. 143, 1744 (1996)
 |
| Appunti su: |
|
| Appunti Biologia |  |
| Tesine Ingegneria tecnico |  |
| Lezioni Geografia |  |