 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 2425 | Gradito: |
Leggi anche appunti:Relazione sull'astronomiaRELAZIONE SULL'ASTRONOMIA L'astronomia è la scienza che studia i corpi L'energia solareL'energia solare Immagine del Sole in H alpha Le geometrie non euclideeLe geometrie non euclidee La crisi delle certezze Dagli anni '80 del XIX |
 |
 |
La scienza del Caos
La scienza del caos studia i sistemi dinamici non lineari. Un sistema dinamico si dice caotico quando presenta le seguenti caratteristiche:
Sensibilità alle condizioni iniziali: a variazioni infinitesime delle condizioni iniziali corrispondono variazioni finite in uscita. Come esempio banale possiamo riportare quello del fumo di più fiammiferi accesi che in condizioni macroscopicamente molto simili (pressione, temperatura, correnti d'aria) segue traiettorie di volta in volta molto differenti.
Imprevedibilità: non si può prevedere l'andamento del sistema in anticipo.
Infine, le orbite nello spazio delle fasi restano confinate, cioè il sistema non evolve verso l'infinito per nessuna variabile. (Si parla in questo caso di attrattori).
Nei sistemi lineari un piccolo cambiamento nello stato del sistema corrisponde a piccole variazioni nelle serie di numeri. Inoltre è ricavabile una legge evolutiva che descrive con precisione l'evolversi del sistema nel tempo. Ad esempio la mappa lineare:
![]()
è sensibile alle condizioni iniziali (infatti, due valori di x leggermente diversi si evolvono divergendo e aumentando la loro distanza), ma il suo andamento è prevedibile e le variabili evolvono verso l'infinito, cioè dopo un numero sufficientemente alto di passaggi xn diviene maggiore quanto vogliamo. Non presenta dunque un comportamento caotico.
Vi sono tuttavia dei sistemi dinamici detti non lineari che -in quanto dinamici- dipendono dal trascorrere del tempo, ma che -in quanto non lineari- non presentano alcuna legge evolutiva. Non vi è dunque alcuna regola che possa descrivere il comportamento del sistema nel suo immediato futuro. Esempi di questi sistemi sono il gocciolio di un rubinetto, la crescita della popolazione delle specie animali o la dinamica oscillatoria di un pendolo attaccato a un sostegno elastico. Prendiamo ad esempio la mappa non lineare:
![]()
è sensibile alle condizioni iniziali, non ha andamento prevedibile e, per valori di x iniziali tra 0 e 1, rimane confinata in uno spazio finito (tra 0 e 1), quindi esibisce un comportamento caotico. Questa semplice equazione viene chiamata mappa logistica, e descrive matematicamente la crescita di una popolazione nel tempo. Il fatto che il valore di xn sia limitato indica che una qualunque popolazione non può crescere indefinitamente, dal momento che ha a disposizione una quantità di risorse necessariamente limitata.
Un crollo delle certezze
Come abbiamo visto, nel corso dell'ultimo secolo vi è stata una progressiva presa di coscienza del crollo delle certezze. Una alla volta tutte le categorie del pensiero scientifico e filosofico, quei concetti ritenuti immutabili (come il tempo, lo spazio, il rapporto causa-effetto) sono stati messi a dura prova. L'immagine stessa della filosofia e della scienza risulta quindi modificata: il sapere ereditato dall'età moderna -per poter sopravvivere- deve mettere in discussione uno dopo l'altro tutti i suoi fondamenti, ma deve scoprirsi ancora capace di calarsi nella vita reale e rispondere alle domande sempre più pressanti che essa gli pone. La scienza del '900 è dunque caratterizzata da un crollo inesorabile delle certezze e da una crisi profonda dei fondamenti del pensiero scientifico. La scienza deriva in parte la spinta al proprio procedere dal bisogno di rispondere ad alcune esigenze, fra le quali quella di ricreare un'immagine coerente del mondo entro cui viviamo. L'atteggiamento tipico dei grandi fondatori della scienza occidentale, come Galileo o Newton, era quello di sottolineare l'universalità e l'eternità delle leggi che essi ritrovano dispiegate nella natura. Questi uomini cercavano schemi onnicomprensivi, concetti o strutture del pensiero che fossero condivisibili da tutti e quindi unificanti, un criterio generale al cui interno si potesse mostrare che ogni cosa esistente è sistematicamente, logicamente e casualmente connessa con ogni altra. Non dovevano esserci nella scienza degli spazi lasciati aperti per sviluppi spontanei, tutto ciò che accade doveva essere interamente spiegabile. La scienza dell'età moderna si era costituita a partire dalla scoperta di una nuova forma di comunicazione con la natura, nella convinzione che la natura potesse e volesse rispondere veramente ai proprio schemi, alle proprie strutture teoriche irrigidite in leggi. La scienza dei nostri tempi, invece si è spesso interrogata sulla legittimità e l'utilità nel ricercare leggi della natura. Bisogna allora accettare il fatto che non è poi così logico, così prevedibile ed evidente il gioco fra uomo e natura, la quale non vuole comunicare con l'uomo né farsi comprendere, ma semplicemente si mostra nella propria incoerenza, instabilità e caoticità. "Se conoscessimo tutte le cause precedenti a ciascun fenomeno naturale, saremmo in grado di prevedere anche il più piccolo movimento di una foglia e determinare quando e come sboccerà ciascun fiore della Terra, ma siccome nella natura è presente un imponderabile elemento di casualità, quella foglia e quel fiore potrebbero sorprenderci con eventi imprevisti" (James Gleick, "CAOS: la nascita di una nuova scienza"). Il contesto entro cui la scienza contemporanea parla di una scoperta della complessità si individua così nella scoperta del carattere imprevedibile di alcuni fenomeni. Se le leggi non ci dicono nulla di preciso e affidabile riguardo il verificarsi del fenomeno nello spazio e nel tempo, se sono ormai soltanto la descrizione di una possibilità che le cose accadano, allora la scienza si riduce ad essere solo uno dei possibili discorsi sul mondo, non più come l'unico esatto. Siamo passati così da un'immagine della scienza come sicurezza, raggiungimento della verità, alla scienza come fallibile.
Spazio delle fasi, attrattori e Butterfly effect
Uno strumento potente per descrivere il comportamento dei sistemi caotici è lo spazio delle fasi, una delle invenzioni più efficaci della scienza moderna. Lo spazio delle fasi fornisce un modo per trasformare i numeri in immagini, astraendo ogni piccola parte di informazione essenziale da un sistema mobile e disegnando un grafico che permette un'analisi visiva del comportamento del sistema in esame. Se il sistema ha due sole variabili la geometria cartesiana è l'ideale per la rappresentazione del moto.
Abbiamo visto come in un sistema non lineare piccole differenze nelle condizioni iniziali possono causare variazioni non prevedibili nel comportamento successivo. Sistemi di tale tipo possono presentare comportamento caotico solo in alcuni tratti, o non presentarlo affatto, o da una situazione apparentemente lineare avere una progressione esponenzialmente divergente.
A partire da tali comportamenti è stato inserito il
concetto di attrattore. In matematica, "un
attrattore è ciò verso cui è attratto il comportamento di un sistema", come afferma
A.K. Dewdney A.K. ("Alla scoperta delle strane attrattive del caos", Le Scienze n°229). Prendiamo un comune
pendolo che si muove sottostando a forze di attrito, che lo rallentano fino a
farlo fermare. Si può descrivere il movimento del pendolo utilizzando un
diagramma di fase, in cui vengono rappresentati su un asse l'angolo del pendolo
con la verticale e sull'altro la velocità con cui cambia l'angolo. Il moto
oscillante del pendolo è rappresentato da un punto che gira attorno all'origine
del diagramma di fase; man mano che il pendolo perde energia, il punto si
avvicina a spirale all'origine, dove infine va a fermarsi. In questo caso
l'origine viene chiamata un attrattore perché sembra attrarre il punto in
movimento nel diagramma di fase. Leggermente più complesso è l'attrattore
insito nel movimento di una pendola a muro, in cui un meccanismo di scappamento
fornisce energia al pendolo impedendogli di rallentare. Se si fa partire
l'orologio con una spinta troppo energica al pendolo, questo rallenta fino al
ritmo prescritto dallo scappamento ma poi non rallenta più. Se invece si avvia
l'orologio con una spinta troppo debole, il pendolo rallenta fino a fermarsi.
Nel caso della spinta troppo energica, il moto del pendolo in un diagramma di
fase è una spirale che si muove a spire sempre più strette attorno a un'orbita
circolare. 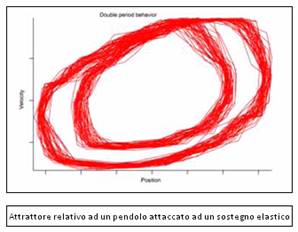 L'attrattore qui è una curva circolare. Si può
far assumere a un comune pendolo un comportamento caotico introducendo un
movimento di vibrazione verticale: se con un motore elettrico si sposta su è
giù in modo sinusoidale il punto di sostegno, è possibile che il pendolo inizi
a oscillare in modo scomposto senza mostrare più alcun comportamento periodico.
Dal
punto di vista geometrico, quindi, abbiamo visto che un attrattore può essere
un punto o una curva. Tuttavia può assumere anche forme più complicate, dotate
di una struttura frattale, e in tal caso si parla di attrattore strano.
L'attrattore qui è una curva circolare. Si può
far assumere a un comune pendolo un comportamento caotico introducendo un
movimento di vibrazione verticale: se con un motore elettrico si sposta su è
giù in modo sinusoidale il punto di sostegno, è possibile che il pendolo inizi
a oscillare in modo scomposto senza mostrare più alcun comportamento periodico.
Dal
punto di vista geometrico, quindi, abbiamo visto che un attrattore può essere
un punto o una curva. Tuttavia può assumere anche forme più complicate, dotate
di una struttura frattale, e in tal caso si parla di attrattore strano.
 Concentriamoci ora sui sistemi in cui da una
situazione apparentemente lineare si ha una progressione esponenzialmente
divergente. È proprio nell'analisi di questi ultimi che si parla di Butterfly Effect. Il cosiddetto
Butterfly Effect deve i suoi natali al meteorologo e scienziato Edward Lorenz
(23 maggio 1917- 08 aprile 2008) che il 29 dicembre 1979 presentò alla
Conferenza annuale dell'American Associaton for the Advancement of Science una
relazione dal titolo "Does a flap of a butterfly's wings in Brazil set off a
Tornado in texas?" (È possibile che il
battito d'ali di una farfalla in Brasile sia in grado di provocare un uragano
in Texas?). Il Butterfly Effect
descrive la crescita esponenziale delle perturbazioni a causa di una variazione
nelle condizioni iniziali. Un piccolo errore nella misura delle condizioni
iniziali o una piccola variazione delle stesse, cresce esponenzialmente con il
tempo, producendo un radicale cambiamento dei risultati.
Concentriamoci ora sui sistemi in cui da una
situazione apparentemente lineare si ha una progressione esponenzialmente
divergente. È proprio nell'analisi di questi ultimi che si parla di Butterfly Effect. Il cosiddetto
Butterfly Effect deve i suoi natali al meteorologo e scienziato Edward Lorenz
(23 maggio 1917- 08 aprile 2008) che il 29 dicembre 1979 presentò alla
Conferenza annuale dell'American Associaton for the Advancement of Science una
relazione dal titolo "Does a flap of a butterfly's wings in Brazil set off a
Tornado in texas?" (È possibile che il
battito d'ali di una farfalla in Brasile sia in grado di provocare un uragano
in Texas?). Il Butterfly Effect
descrive la crescita esponenziale delle perturbazioni a causa di una variazione
nelle condizioni iniziali. Un piccolo errore nella misura delle condizioni
iniziali o una piccola variazione delle stesse, cresce esponenzialmente con il
tempo, producendo un radicale cambiamento dei risultati.
 Dal punto di vista
dell'orbita del sistema nello spazio delle fasi, un sistema caotico presenta
spesso una dinamica caratterizzata da un attrattore strano, ma ciò non è da
considerarsi una regola assoluta. Mentre un attrattore tradizionale descrive la
probabilità di presenza del sistema in un punto in un determinato istante di
tempo, in un attrattore strano non si può conoscere analiticamente dove il
sistema si sarà posizionato al dato istante di tempo. Oltre a essere molto più
complessi di quelli tradizionali, gli attrattori strani sono caratterizzati dal
fatto che non ritornano mai su se stessi, in quanto il sistema non è periodico
e non si ripresenta mai con caratteristiche uguali. Tra gli attrattori strani
il più famoso fu ipotizzato da Edward Lorenz nel 1963, nella cui proiezione
bidimensionale si presenta molto simile a una farfalla. Egli studiò un sistema
relativamente semplice: una ruota idraulica. Essa viene messa in moto da un
flusso d'acqua che cadendo ne riempie i secchi: se tale flusso è abbastanza
veloce, la ruota comincerà a muoversi regolarmente con velocità costante. Se
aumentiamo ancor più la velocità, assisteremo a fenomeni caotici: alcuni secchi
non
Dal punto di vista
dell'orbita del sistema nello spazio delle fasi, un sistema caotico presenta
spesso una dinamica caratterizzata da un attrattore strano, ma ciò non è da
considerarsi una regola assoluta. Mentre un attrattore tradizionale descrive la
probabilità di presenza del sistema in un punto in un determinato istante di
tempo, in un attrattore strano non si può conoscere analiticamente dove il
sistema si sarà posizionato al dato istante di tempo. Oltre a essere molto più
complessi di quelli tradizionali, gli attrattori strani sono caratterizzati dal
fatto che non ritornano mai su se stessi, in quanto il sistema non è periodico
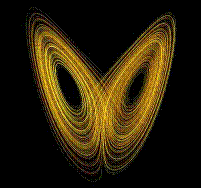
e non si ripresenta mai con caratteristiche uguali. Tra gli attrattori strani
il più famoso fu ipotizzato da Edward Lorenz nel 1963, nella cui proiezione
bidimensionale si presenta molto simile a una farfalla. Egli studiò un sistema
relativamente semplice: una ruota idraulica. Essa viene messa in moto da un
flusso d'acqua che cadendo ne riempie i secchi: se tale flusso è abbastanza
veloce, la ruota comincerà a muoversi regolarmente con velocità costante. Se
aumentiamo ancor più la velocità, assisteremo a fenomeni caotici: alcuni secchi
non 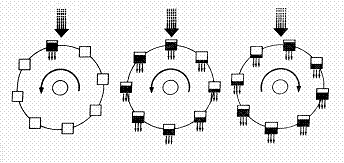 riusciranno a riempirsi,
perciò ravviseremo rallentamenti del moto o addirittura inversioni dello
stesso, senza alcuna possibilità di previsione. L'attrattore era stabile, aveva
un piccolo numero di dimensioni ed era aperiodico, non poteva mai intersecare
se stesso perché, se lo avesse fatto, sarebbe tornato a un punto già visitato e
da lì in avanti il moto si sarebbe ripetuto in un ciclo periodico. Ciò non
accadeva mai. Il diagramma rivelava una sorta d'infinita complessità: il
movimento rimaneva sempre entro certi limiti, non uscendone mai. Esso tracciava
una strana figura tipica, una sorta di doppia spirale a tre dimensioni, simile
ad una farfalla con le ali aperte. La forma segnalava un puro disordine, dal
momento che nessun punto o sistema di punti si ripeteva mai. Eppure segnalava
anche una nuova sorta di ordine: disegnava di continuo nuove spire; quelle
curve, quelle spirali erano infinitamente profonde. Il moto sull'attrattore è
astratto ma dà il senso del moto del sistema reale: il passaggio da un'ala
dell'attrattore all'altra corrisponde a un'inversione nella direzione di
rotazione della ruota idraulica.
riusciranno a riempirsi,
perciò ravviseremo rallentamenti del moto o addirittura inversioni dello
stesso, senza alcuna possibilità di previsione. L'attrattore era stabile, aveva
un piccolo numero di dimensioni ed era aperiodico, non poteva mai intersecare
se stesso perché, se lo avesse fatto, sarebbe tornato a un punto già visitato e
da lì in avanti il moto si sarebbe ripetuto in un ciclo periodico. Ciò non
accadeva mai. Il diagramma rivelava una sorta d'infinita complessità: il
movimento rimaneva sempre entro certi limiti, non uscendone mai. Esso tracciava
una strana figura tipica, una sorta di doppia spirale a tre dimensioni, simile
ad una farfalla con le ali aperte. La forma segnalava un puro disordine, dal
momento che nessun punto o sistema di punti si ripeteva mai. Eppure segnalava
anche una nuova sorta di ordine: disegnava di continuo nuove spire; quelle
curve, quelle spirali erano infinitamente profonde. Il moto sull'attrattore è
astratto ma dà il senso del moto del sistema reale: il passaggio da un'ala
dell'attrattore all'altra corrisponde a un'inversione nella direzione di
rotazione della ruota idraulica.
I frattali
 I frattali, gli oggetti geometrici che
descrivono il caos, sono equazioni o sistemi di equazioni non lineari, di grado
superiore al primo che, iterate migliaia di volte, danno origine a forme
particolarmente complesse, frastagliate ed irregolari non appartenenti alla
geometria euclidea.
I frattali, gli oggetti geometrici che
descrivono il caos, sono equazioni o sistemi di equazioni non lineari, di grado
superiore al primo che, iterate migliaia di volte, danno origine a forme
particolarmente complesse, frastagliate ed irregolari non appartenenti alla
geometria euclidea.
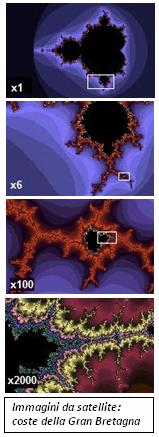
Una delle caratteristiche più importanti dei frattali è l'autosomoglianza: osservando un frattale notiamo che esso ha una certa struttura spaziale, in generale piuttosto complicata e con dettagli che a occhio nudo non riusciamo a distinguere. Se utilizziamo una lente di ingrandimento per osservare meglio tali dettagli, noteremo che ognuno riproduce quasi esattamente la stessa struttura spaziale dell'oggetto non ingrandito. In altre parole l'immagine iniziale si ripete infinite volte a scale sempre più piccole. Tale peculiarità è presente molto spesso in natura ecco perciò il motivo della loro vasta applicazione nella descrizione di montagne, piante, nuvole o linee costiere.
Altro elemento degno di nota è la loro dimensione frazionata. Normalmente siamo abituati a trattare con oggetti geometrici la cui dimensione è espressa con un numero naturale: il punto ha dimensione zero, una linea ha dimensione 1, una figura piana 2 e un solido ha dimensione 3. Per caratterizzare i frattali, invece, si ricorre a un nuovo concetto di dimensione, per cui la dimensione degli oggetti sarà un numero razionale. I frattali, infatti, stanno a metà fra une certa dimensione e la successiva. Per esempio vi è un frattale (la Curva di Koch) costituito da una linea di lunghezza infinita che racchiude una porzione di spazio finita: in questo caso l'oggetto è più di una linea ma meno di un piano, quindi è ragionevole pensare che la sua dimensione sia un numero compreso fra 1 e 2. La dimensione frattale (o dimensione di Hausdorff) è un parametro di estrema importanza che determina il 'grado di irregolarità' dell'oggetto frattale preso in esame.
"Le nuvole non sono sfere, ama dire Mandelbrot. Le montagne non sono coni. Il fulmine non si propaga in linea retta. La nuova geometria riflette un universo che è irregolare, non è arrotondato; è scabro, non liscio. È una geometria del bucherellato, del butterato e rotto, del contorto, aggrovigliato e intrecciato. Per comprendere la complessità della natura era necessario che prendesse forma il sospetto che la casualità non fosse solo qualcosa di casuale, di accidentale." (James Gleick, "CAOS: la nascita di una nuova scienza")
Mandelbrot: il padre dei frattali
Il nome frattale è stato coniato da Beniot Mandelbrot nel 1975, il quale fece derivare il termine dal latino "fractus" cioè frammentato, frastagliato, irregolare. La storia di questo personaggio è piuttosto curiosa e si avvicina a quella di molti grandi scienziati osteggiati dall'élite culturale del proprio tempo. Egli, infatti, rimase a lungo ai margini della "scienza ortodossa", in quanto adottò un approccio non convenzionale alla matematica. Egli stesso si definì "un pioniere per necessità" e un "nomade per scelta" e, in particolare, egli fuggì dalla Francia nel periodo in cui rivestiva un ruolo di primaria importanza Bourbaki, pseudonimo dietro cui si nascondeva un gruppo di matematici "puristi all'eccesso", costituitosi con lo scopo di conferire alla matematica il primato sulle altre scienze, estremizzandone le caratteristiche di austerità e formalità e rifiutando l'uso di immagini. I primi studi furono svolti da Mandelbrot sui dati riguardanti i prezzi del cotone. Egli si accorse che le variazioni di prezzo erano casuali e imprevedibili, ma la sequenza dei mutamenti era indipendente dalla scala: le curve per le variazioni giornaliere e mensili dei prezzi coincidevano perfettamente. Da dati estremamente disordinati derivava un tipo di ordine inatteso.
Successivamente egli si imbatté in un problema pratico di grande interesse per l'IBM, la società presso cui lavorava. Gli ingegneri erano imbarazzati dal problema del rumore nelle linee telefoniche usate per trasmettere informazioni da un computer all'altro. La corrente elettrica trasporta le informazioni in pacchetti discreti e gli ingegneri sapevano che quanto più intensa avessero reso la corrente, tanto migliore essa sarebbe stata per combattere il rumore; tuttavia sperimentalmente c'erano rumori spontanei che non potevano mai essere eliminati e che talvolta coprivano una parte di segnale producendo un errore. Benché per sua natura il rumore di trasmissione fosse causale, si era notato che esso si presentava a gruppi: i periodi di comunicazione senza errori erano seguiti da periodi di errori. Mandelbrot fornì un modo per descrivere la distribuzione degli errori che prediceva esattamente i modelli di distribuzione osservati, ma che rendeva impossibile calcolare una media degli errori poiché essi tendevano ad una dispersione infinita. Egli fu in grado di introdurre separazioni sempre più profonde tra i periodi di trasmissione pulita e quelli di errori. Supponiamo di dividere un giorno in ore: un'ora può trascorrere senza errori, poi un'ora potrebbe contenere errori, poi un'altra potrebbe avere nuovamente errori. A questo punto immaginiamo di dividere l'ora con errori in periodi minori di venti minuti: anche in questo caso troveremo periodi privi di errori ed altri con errori. Mandelbrot sostenne, contrariamente all'intuizione, che non si possa mai trovare un tempo in cui gli errori siano disseminati in modo continuo: all'interno di ogni gruppo di errori, per quanto breve, ci saranno sempre periodi di trasmissione completamente privi di errori. Inoltre Mandelbrot scoprì che su scale di un'ora o di un secondo la proporzione dei periodi privi di errori rispetto ai periodi con errori restava costante.
Questa descrizione di Mandelbrot riproduceva la costruzione dell'insieme di Cantor, risalente alla fine dell'Ottocento. Consideriamo l'intervallo dei numeri compresi tra 0 e 1, rappresentato da un segmento; immaginiamo poi di dividere il segmento in tre parti uguali e di togliere quella centrale: rimangono due segmenti, con ciascuno dei quali si procede allo stesso modo usato col segmento d'origine. Rimangono così quattro segmenti, ciascuno dei quali si toglie la parte centrale e così all'infinito. Al termine del processo rimane una "polvere" di punti disposti in gruppi, in numero infinitamente grande e infinitamente disperso, ovvero un numero di segmenti tendente all'infinito, ciascuno di essi di lunghezza tendente a zero. Pertanto sembra ragionevole pensare che la dimensione dell'insieme di Cantor sia inferiore a 1 (dimensione della retta) ma sia superiore a 0 (dimensione di un insieme infinito di punti).
Dopo 5 iterazioni l'insieme di Cantor risulta essere così costruito:

Tornando al problema della trasmissione dei segnali, Mandelbrot pensava agli errori di trasmissione come a insiemi di Cantor distribuiti nel tempo. Tale teoria suggerì che, anziché tentare di aumentare l'intensità del segnale per sopraffare il rumore, era più ragionevole inviare un segnale modesto accettando l'inevitabilità degli errori e usando una strategia di ridondanza per individuarli e correggerli.
Il fiocco di neve di Von Koch
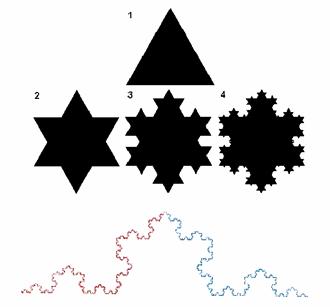 Un altro famoso frattale è il fiocco di neve di Van Koch. Per costruirlo si prenda un
triangolo equilatero (1) e si divida ogni suo lato in tre parti uguali, si
tolga quella centrale e si costruisca al suo posto un triangolo equilatero. Il
risultato sarà una stella di Davide (2). Ripetendo questa operazione
all'infinito si otterrà una figura simile a un fiocco di neve, nota come la curva di Koch, da Helge von Koch, il matematico svedese
che la descrisse per primo nel 1904.
Un altro famoso frattale è il fiocco di neve di Van Koch. Per costruirlo si prenda un
triangolo equilatero (1) e si divida ogni suo lato in tre parti uguali, si
tolga quella centrale e si costruisca al suo posto un triangolo equilatero. Il
risultato sarà una stella di Davide (2). Ripetendo questa operazione
all'infinito si otterrà una figura simile a un fiocco di neve, nota come la curva di Koch, da Helge von Koch, il matematico svedese
che la descrisse per primo nel 1904.
La curva di Koch presenta diversi aspetti interessanti. Da un lato, essa è una curva continua, che non interseca mai se stessa, perché i nuovi triangoli costruiti su ciascun lato sono sempre abbastanza piccoli da evitare di urtarsi tra loro. Ogni trasformazione aggiunge una piccola area all'interno della curva, ma l'area totale riamane finita e non molto più grande del triangolo originario. Se tracciassimo un cerchio circoscritto attorno al triangolo originario, la curva di Koch non si estenderebbe mai oltre a esso. Eppure la curva in sé ha una lunghezza infinita, la stessa lunghezza di una linea retta euclidea, che si estenda fino ai confini di un universo illimitato. Questo risultato paradossale, una lunghezza infinita in uno spazio finito, turbò molti dei matematici di inizio secolo in quanto la curva di Koch era come un "mostro" irrispettoso nei confronti di qualsiasi ragionevole intuizione sulle figure geometriche.
 |
| Appunti su: ruota idraulica lorenz, |
|
| Appunti Geografia |  |
| Tesine Ecologia ambiente |  |
| Lezioni Archeologia |  |