 |
|
| Appunti scientifiche |
|
 |
|
| Appunti scientifiche |
|
| Visite: 1707 | Gradito: |
Leggi anche appunti:La geometria descritivaLA GEOMETRIA DESCRITIVA Sempre si è fatto uso del disegno per rappresentare Applicazioni delle geometrie non euclideeAPPLICAZIONI DELLE GEOMETRIE NON EUCLIDEE L'importanza delle geometrie non NUOVI TEOREMI per la nuova geometriaNUOVI TEOREMI per la nuova geometria Quali teoremi Bolyai e Lobacevskij riuscirono |
 |
 |
L'importanza dell'analisi infinitesimale nelle applicazioni scientifiche sperimentali
Tra tutti gli innumerevoli settori di cui è costituito il complesso del sapere matematico, sicuramente uno dei più ostici (e perciò entusiasmanti) dal punto di vista teorico e, al tempo stesso, uno dei più fecondi in termini di applicazioni scientifico-sperimentali, è quello dell'Analisi Infinitesimale (che, come abbiamo visto nella seconda sezione, ha dato del filo da torcere ai matematici ottocenteschi che ne cercavano una necessaria fondazione rigorosa).
Si può dire che l'analisi infinitesimale reale si occupa, in buona sostanza, dello studio delle funzioni reali di variabile indipendente reale, delle quali, a partire dalla legge che caratterizza ciascuna di esse, vengono determinati, tra gli altri aspetti: i punti o gli intervalli di definizione (domini delle funzioni); eventuali simmetrie del grafico cartesiano rispetto agli assi coordinati; comportamento in prossimità dei punti di non-definizione e "all'infinito"; intervalli di continuità; punti di discontinuità (e relative specie); intervalli in cui la funzione cresce o decresce; punti nei quali non è possibile quantificare la crescita o la decrescita della funzione (punti di non derivabilità) ; punti le cui ordinate presentano valori massimi o minimi relativamente ad un determinato intervallo considerato (i "punti di massimo" e "di minimo"); concavità della curva grafico della funzione; punti "di flesso", nei quali si registra un cambiamento della concavità della curva (da verso l'alto a verso il basso e viceversa); misura dell'area sottesa alla curva grafico della funzione in un determinato intervallo di valori della variabile indipendente. Da questi dati, ottenuti mediante l'uso di importantissimi operatori (quali limiti, derivate, integrali indefiniti e definiti), si riesce quindi ad evincere tutto quello che caratterizza l'andamento del grafico della funzione studiata. La potenza dell'analisi in ambito strettamente matematico sta, limitatamente a questi aspetti, proprio nella sua incredibile capacità di prevedere, usando gli operatori di cui sopra, tutte le caratteristiche di una funzione senza tracciarne il grafico (che infatti si rivela essere molto spesso il punto di arrivo dello stesso studio di funzione).
Tuttavia, è a livello applicativo che questa branca della matematica mostra la sua notevole utilità; infatti, le relazioni causa-effetto che determinano i fenomeni della natura devono essere esprimibili, secondo il metodo scientifico galileiano, attraverso relazioni matematiche tra le grandezze che concorrono ai fenomeni, ossia attraverso funzioni. Pertanto, studiare funzioni dotate di particolari significati fisici, chimici, biologici etc. permette, in definitiva, di conoscere matematicamente anche le caratteristiche dei rapporti causa-effetto sui quali sono basati tutti i meccanismi della Natura.
Inoltre, i rapporti esistenti tra i concetti di funzione primitiva, funzione derivata e integrale indefinito, permettono di dedurre, a partire da determinate equazioni coinvolgenti la derivata di una funzione (dette equazioni differenziali), espressioni matematiche che esplicitano la funzione stessa: questo, come avremo modo di approfondire nel seguito, è molto utile nei casi in cui si voglia determinare l'equazione di una funzione f(x) conoscendone alcune caratteristiche che siano correlate all'operatore derivata.
Per questi motivi, si capisce dunque l'enorme importanza, ai fini della comprensione scientifica del mondo, degli strumenti offerti dall'Analisi Infinitesimale: tra questi, in primo luogo, vi sono i già citati operatori derivata, integrale indefinito, integrale definito, per ognuno dei quali daremo ora brevemente delle definizioni non propriamente rigorose, in quanto volte soprattutto ad enuclearne le funzioni e le relazioni tra essi alle quali rimanderemo nel seguito della trattazione.
Per derivata di una funzione f(x) s'intende il limite del
rapporto incrementale della funzione f(x), relativo ad un
generico punto di ascissa x appartenente al dominio di f(x)
e ad un certo incremento h dato al punto x (tale che anche il
punto di ascissa x + h appartenga al dominio della funzione), per h
tendente a zero. In simboli si ha: ![]() , dove i simboli f'(x) e
, dove i simboli f'(x) e ![]() indicano indifferentemente appunto la derivata (prima) della
funzione f(x).
indicano indifferentemente appunto la derivata (prima) della
funzione f(x).
L'importanza della derivata nello studio di funzione e nelle applicazioni scientifiche ad esso connesse, risiede proprio nella sua definizione: infatti, se il rapporto incrementale quantifica una variazione dei valori assunti dalla funzione relativamente ad un ben definito intervallo di valori della variabile indipendente, la derivata, facendo tendere a 0 l'ampiezza del suddetto intervallo, è come se quantificasse una variazione punto per punto dei valori di f(x); proprio per questa sua proprietà, la derivata viene considerata anch'essa una funzione di x, che associa ad ogni x appartenente al dominio della funzione f(x) un determinato valore che quantifica la crescita o la decrescita "puntuale" di f(x). Questa corrispondenza tra la crescita del grafico di f(x) e la sua derivata viene, come vedremo negli esempi successivi, molto utilizzata nelle applicazioni fisiche, biologiche etc. , nelle quali solitamente si analizza una variazione nel tempo dei valori di determinate grandezze funzioni del tempo.
Per integrale indefinito s'intende invece un operatore che, agendo inversamente alla derivata, associa ad una funzione f(x), detta funzione integranda, la totalità delle funzioni primitive di f(x) (ossia funzioni che derivate danno f(x) ). L'integrale indefinito è dunque l'operatore che permette di risalire dalla derivata comune di infinite funzioni alle funzioni stesse, la cui espressione rientra, al variare di C in R, nella forma generale F(x) + C ed è determinata, per ognuna di esse, da un preciso valore di C.
In simboli la definizione di integrale indefinito (indicato col simbolo ![]() ) è la seguente:
) è la seguente:
![]() .
.
L'integrale definito (di cui per brevità non diamo qui alcuna definizione rigorosa) è invece un altro operatore, differente dall'integrale indefinito ma ad esso correlato, che presenta due importantissime funzioni. In primo luogo, esso permette il calcolo della misura dell'area del trapezoide sotteso alla curva del grafico di una funzione, limitatamente ad un certo intervallo di valori della variabile indipendente (aspetto, questo, molto importante dal punto di vista applicativo, in quanto molto spesso anche all'area del trapezoide corrisponde una particolare grandezza fisica, ad es. il lavoro di una forza o l'energia). In secondo luogo, l'integrale definito, in virtù della stretta relazione tra funzione integrale (quest'ultima derivante dal concetto di integrale definito) e integrale indefinito discendente dal teorema fondamentale del calcolo integrale, consente di risolvere le già citate equazioni differenziali "sostituendo", dunque, la funzione dell'integrale indefinito come operatore inverso della derivata (in realtà non vi è vera sostituzione, in quanto l'integrale indefinito è comunque applicato nel calcolo di un integrale definito). Come vedremo, la risoluzione delle equazioni differenziali mediante gli integrali definiti si rivela molto utile ed importante in ambiti scientifici extramatematici, nei quali è necessario risalire a particolari primitive mediante integrazioni in specifici intervalli, dotati di un loro proprio significato all'interno delle varie scienze.
Il simbolo dell'integrale definito di una funzione f(x)
relativo ad un intervallo di estremi a e b , con b>a, è
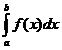 .
.
Dopo aver descritto in via teorica l'importanza dell'Analisi Infinitesimale nelle scienze sperimentali, passiamo ora in rassegna alcuni esempi, presi dagli ambiti della Biologia e della Fisica, nei quali essa è applicata con successo per descrivere i fenomeni naturali in termini di funzioni.
 |
| Appunti su: funzioni e applicazioni scientifiche, |
|
| Appunti Geografia |  |
| Tesine Contabilita |  |
| Lezioni Statistica |  |